Parabol
1. Khái niệm Parabol
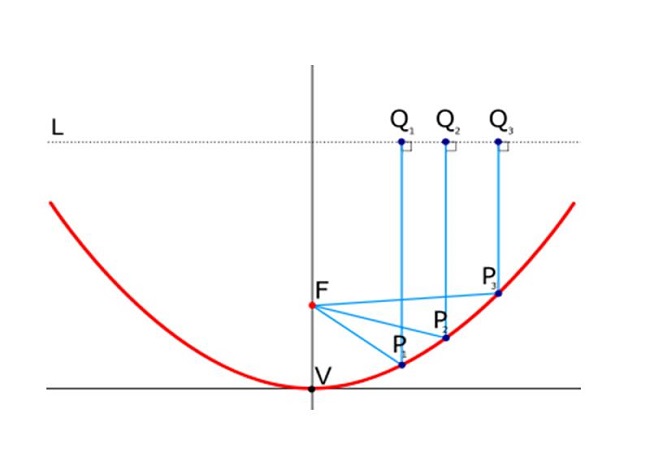
- Điểm F được coi là tiêu điểm của Parabol
- Đường thẳng Δ được gọi là đường chuẩn của parabol.
- Khoảng cách từ F tới Δ được gọi là thông số tiêu của parabol.
Một parabol chỉ sở hữu một trục đối xứng duy nhất, đi qua tiêu điểm và vuông góc với đường chuẩn của nó. Giao điểm của trục này và parabol được gọi là đỉnh. Một parabol quay xung quanh trục của nó trong ko gian ba chiều sẽ tạo ra một hình paraboloid.
2. Phương trình Parabol
2.1 Phương trình tổng quát của Parabol
Dạng tổng quát của phương trình Parabol sở hữu dạng:
(Ax + By)2 + Cx + Dy + E = 0
Phương trình này được rút ra từ phương trình tổng quát của những đường Conic và tính chất của đường parabol.
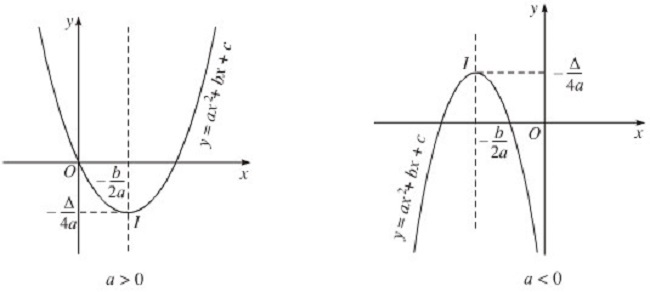
Trong thực thế, ta sở hữu thể thấy đường parabol là đồ thị của hàm số bậc 2 sở hữu dạng: y = ax2+ bx + c.Trong đó:
- Hoành độ của tiêu điểm x = -b2a
- Thay x vào phương trình tổng quát ta tính được y = c -b2 -14a
2.2 Phương trình chính tắc của Parabol
Phương trình chính tắc của Parabol được trình diễn dưới dạng:
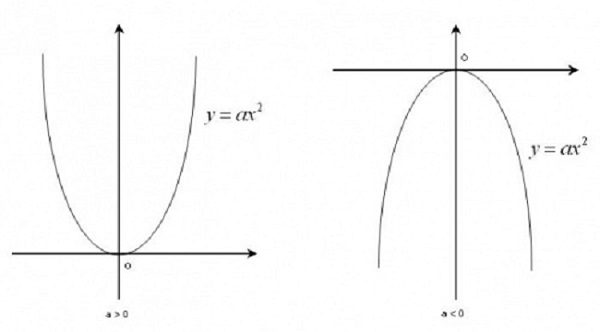
y2 = 2px (với p >0)
3. Cách vẽ Parabol
3.1 Cách vẽ Parabol bằng thước và compa
- Bước 1: Khảo sát những điểm thuộc Parabol (Vì Parabol là đường đối xứng nhau nên chúng ta chỉ cần khảo sát 1 nửa parabol)
- Bước 2: Xác định trục đối xứng của Parabol (Kẻ đường thẳng đi qua điểm F cho trước và vuông góc với đường chuẩn), gọi giao điểm là O
- Bước 3: Lấy M là trung điểm của OF, tìm một điểm M1 bất kỳ thuộc đoạn MF. Kẻ đường thẳng đi qua M1 và track track với đường thẳng cho trước.
- Bước 4: Tiêu dùng Compa, quay 1 cung sở hữu bán kính OM1, cung và đường thẳng qua M1 cắt nhau ở đâu, ta được 1 điểm thuộc Parabol.
- Bước 5: Lấy thêm những điểm bất kỳ thuộc đoạn MF rồi làm tương tự những bước trên.
- Cuối cùng, ta nối những điểm thuộc parabol, là tạo thành đường parabol hoàn chỉnh.
3.2 Cách vẽ parabol thông qua đồ thị hàm số bậc 2
Trên thực tế, cách vẽ trên ko được ứng dụng nhiều, thay vào đó, người ta thường trình diễn parabol thông qua đồ thị hàm số bậc 2. Dưới đây mình sẽ giới thiệu cách vẽ hàm số bậc 2 nhé! Ví dụ hàm số bậc 2 sở hữu dạng: y = ax2 + bx + c (a # 0)
- Bước 1: Xác định tọa độ của đỉnh, hoành độ x = -b2a, tung độ y = -4a(một cách dễ dàng hơn, sau lúc tính được hoành độ x, ta thay vào phương trình sẽ tim ra tung độ y.
- Bước 2: Vẽ trục đối xứng (đi qua đỉnh và track track với trục tung)
- Bước 3: Tìm một số điểm đặc trưng thuộc đồ thị hàm số. Đơn thuần khách hàng chỉ cần tìm những giá trị khác nhau của x, thay vào phương trình sẽ tìm ra y. Người mua nên tìm khoảng 5 tới 7 điểm khác nhau thuộc đồ thị hàm số, càng nhiều điểm thì độ xác thực càng cao. Sau đó nối những điểm vào với nhau là được đồ thị hàm số bậc 2 là một đường parabol.
Cách vẽ khá dễ dàng mà còn được vận dụng rất nhiều trong toán, đặc trưng là trong những đề thi ko thể thiếu những câu hỏi về đồ thị hàm số, khách hàng lưu ý nhé!
4. Cách viết phương trình Parabol
- Cho Parabol đi qua một điểm một mực A(x0,y0), ta sở hữu y = ax02 + bx0 + c
- Cho biết tọa độ đỉnh I(x0,y0), thay tọa độ vào công thức đỉnh ứng với những hệ số
- Cho biết trục đối xứng là x = x0, ta sở hữu x0 = -b2a
5. Ứng dụng của Parabol trong cuộc sống
5.1 Ứng dụng của parabol trong ngành xây dựng
Trong xây dựng, ta sở hữu thể bắt gặp nhiều ứng dụng của parabol, ví như lúc xây cầu, để giảm lực tác động lên cây cầu và lực được chia đều sang 2 bên chân cầu thay vì giữa cầu, người ta sẽ thiết kế cầu sở hữu hình dạng Parabol sở hữu bề lõm quay xuống dưới. Lý thuyết vận dụng là lúc mặt cầu sở hữu dạng Parabol thì hướng xe đi sẽ theo phương tiếp tuyến với mặt cầu, làm giảm lực của xe tác dụng lên mặt cầu, từ đó cầu sẽ cứng cáp và khó bị sập hơn.
Một ứng dụng khác của Parabol trong xây dựng là những đường ray tàu siêu tốc tại những khu vui chơi tiêu khiển. Những cung đường cong hình Parabol sẽ làm tăng trải nghiệm cho người chơi, tạo nên những vòng cua mạo hiểm hơn, quan yếu nó giúp tạo động lực khiến cho tàu di chuyển.
5.2. Ứng dụng của parabol trong việc cung cấp mặt kính
Nghĩ tới Parabol tưởng đâu là một tri thức toán học khó nhằn và xa lạ, nhưng hình ảnh về Parabol luôn xuất hiện quanh chúng ta. Cụ thể nó được ứng dụng trong gia công kính thiên văn và gương cầu. Việc thiết kế đèn pin, đèn pha ô tô xe máy dạng mặt cầu Parabol sẽ làm tăng khả năng phát sáng và lan tỏa ánh sáng.
5.3. Ứng dụng của parabol tiêu dùng làm Anten Parabol
Anten parabol là một anten sử dụng một gương phản xạ parabol, một bề mặt cong với hình dạng cắt ngang của một parabol, để định hướng sóng vô tuyến. Do sở hữu dạng Parabol nên sóng thu về sẽ tập trung hơn, ít bị mất sóng hơn, từ đó tín hiệu sẽ rõ nét hơn, ko bị nhòe.
Ngoài ra, do đường Parabol sở hữu hình cong đối xứng đẹp, người ta thường lấy hình ảnh của Parabol để trang trí như làm cổng chào,…
Trên đây là tổng hợp tri thức cơ bản nhất về Parabol, chúc khách hàng học tập thật tốt và làm chủ được tri thức toán học quan yếu này nhé!