Phương trình của đường thẳng, trắc nghiệm toán học lớp 12 2022

A. Lý thuyết cơ bản

1. Phương trình đường thẳng

2. Vị trí tương đối giữa hai đường thẳng

Cho hai đường thẳng $d$ đi qua $A$ , có $VTCP,,overrightarrow{{{u}_{1}}}=(a;b;c)$ và đường thẳng $d'$ đi qua $B$ và có $VTCP,,overrightarrow{{{u}_{2}}}=(a;b;c)$ .

Khi $d$ và $d'$ có phương trình $d:left{ begin{array}{l}x={{x}_{0}}+at\y={{y}_{0}}+bt\z={{z}_{0}}+ctend{array} right.,,(tin mathbb{R})$ và $d':left{ begin{array}{l}x={{x}_{0}}'+a't\y={{y}_{0}}'+b't\z={{z}_{0}}'+c'tend{array} right.,,(tin mathbb{R})$ .

Khi đó số nghiệm của hệ phương trình $left{ begin{array}{l}{{x}_{0}}+at={{x}_{0}}'+a't\{{y}_{0}}+bt={{y}_{0}}'+b't\{{z}_{0}}+ct={{z}_{0}}'+c'tend{array} right.$ bằng số giao điểm của $d$ và $d'$ .

Trong trường hợp hệ vô nghiệm thì $d$ và $d'$ song song với nhau hoặc chéo nhau. Nếu $overrightarrow{{{u}_{1}}},overrightarrow{{{u}_{2}}}$ cùng phương thì $d$ // $d'$ .

3. Vị trí tương đối giữa đường thẳng và mặt phẳng

Cho mặt phẳng $(P):,Ax+By+Cz+D=0$ và đường thẳng $d:left{ begin{array}{l}x={{x}_{0}}+at\y={{y}_{0}}+bt\z={{z}_{0}}+ctend{array} right.,,(tin mathbb{R})$ .

Xét phương trình $A({{x}_{0}}+at)+B({{y}_{0}}+bt)+C({{z}_{0}}+ct)+D=0$ (ẩn t) (*)

4. Khoảng cách

$d(M,d)=frac{left| left[ overrightarrow{{{M}_{0}}M},overrightarrow{u} right] right|}{|overrightarrow{u}|}$ .

$d({{d}_{1}},{{d}_{2}})=frac{left| left[ overrightarrow{{{u}_{1}}},overrightarrow{{{u}_{2}}} right].overrightarrow{{{M}_{1}}{{M}_{2}}} right|}{left| left[ overrightarrow{{{u}_{1}}},overrightarrow{{{u}_{2}}} right] right|}$ .

5. Góc

B. Bài tập

Dạng 1. Lập phương trình đường thẳng biết VTCP 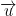$overrightarrow{u}$

A. Phương pháp

B. Bài tập ví dụ

Ví dụ 1.1: Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng $d$ đi qua điểm $M(1;-2;0)$ và có vecto chỉ phương $overrightarrow{u}(0;0;1)$ . Đường thẳng $d$ có phương trình tham số là

A. $left{ begin{array}{l}x=1\y=-2\z=tend{array} right.$ . B. $left{ begin{array}{l}x=1-t\y=-2+2t\z=tend{array} right.$ . C. $left{ begin{array}{l}x=t\y=-2t\z=1end{array} right.$ . D. $left{ begin{array}{l}x=1-2t\y=-2-t\z=0end{array} right.$ .

Lời giải:

Phương trình tham số của đường thẳng $d$ đi qua điểm $M(1;-2;0)$ và có vecto chỉ phương $overrightarrow{u}(0;0;1)$ là $left{ begin{array}{l}x=1\y=-2\z=tend{array} right.$ .

Ví dụ 1.2: Trong không gian với hệ tọa độ $Oxyz$ , cho hai điểm $A(-1;3;-2),,B(-3;7;-18)$ và mặt phẳng $(P)$ có phương trình $2x-y+z+1=0$ . Viết phương trình đường thẳng $d$ đi qua 2 điểm $A,B$ .

A. $left{ begin{array}{l}x=-1-t\y=3+2t\z=-2+8tend{array} right.$ . B. $left{ begin{array}{l}x=-1-t\y=3+2t\z=-2-8tend{array} right.$ . C. $left{ begin{array}{l}x=1-t\y=3+2t\z=-2-8tend{array} right.$ . D. $left{ begin{array}{l}x=-1-t\y=3+2t\z=2-8tend{array} right.$ .

Lời giải:

$overrightarrow{AB}(-2;4;-16)=2(-1;2;-8)$ .

Phương trình tham số của đường thẳng $d$ đi qua điểm $A$ và có vecto chỉ phương $overrightarrow{u}(-1;2;-8)$ là $left{ begin{array}{l}x=-1-t\y=3+2t\z=-2-8tend{array} right.$ .

Chọn đáp án A.

Ví dụ 1.3: Trong không gian với hệ tọa độ $Oxyz$ , cho hai mặt phẳng $(P):x-2y+3z-4=0$ và $(Q):3x+2y-5z-4=0$ . Giao tuyến của $(P)$ và $(Q)$ có phương trình tham số là

A. $left{ begin{array}{l}x=2+2t\y=-1+7t\z=4tend{array} right.$ . B. $left{ begin{array}{l}x=2-2t\y=-1+7t\z=-4tend{array} right.$ . C. $left{ begin{array}{l}x=2+2t\y=1+7t\z=4tend{array} right.$ . D. $left{ begin{array}{l}x=1+2t\y=1-7t\z=4tend{array} right.$ .

Lời giải:

Cách 1:

Xét hệ $left{ begin{array}{l}x-2y+3z-4=0\3x+2y-5z-4=0end{array} right.,,,(*)$ .

Cho $x=0$ thay vào (*) tìm được $y=-8,z=-4$ .

Đặt $A(0;-8;-4)$ .

Cho $z=0$ thay vào (*) tìm được $x=2,y=-1$ .

Đặt $B(2;-1;0)Rightarrow overrightarrow{AB}(2;7;4)$ là một vecto chỉ phương của $(P)cap (Q)$ .

Như vậy, phương trình tham số của $(P)cap (Q)$ là $left{ begin{array}{l}x=2+2t\y=-1+7t\z=4tend{array} right.$ .

Cách 2:

Xét hệ $left{ begin{array}{l}x-2y+3z-4=0\3x+2y-5z-4=0end{array} right.,,(*)$ .

Cho $z=0$ thay vào (*) tìm được $x=2,y=-1$ .

Đặt $B(2;-1;0)$ .

$(P):x-2y+3z-4=0$ có vecto pháp tuyến $overrightarrow{{{n}_{P}}}=(1;-2;3)$ .

$(Q):3x+2y-5z-4=0$ có vecto pháp tuyến $overrightarrow{{{n}_{Q}}}(3;2;-5)$ .

$Rightarrow left[ overrightarrow{{{n}_{P}}},overrightarrow{{{n}_{Q}}} right]=(4;14;8)Rightarrow$ chọn $overrightarrow{u}=(2;7;4)$ là một vecto pháp tuyến của $(P)cap (Q)$ .

Như vậy, phương trình tham số của $(P)cap (Q)$ là $left{ begin{array}{l}x=2+2t\y=-1+7t\z=4tend{array} right.$ .

Chọn đáp án A.

Ví dụ 1.4 (THPT Chuyên KHTN 2017 Lần 4) Trong không gian với hệ tọa độ $Oxyz$ , cho ba điểm $A(2;-1;0),B(-1;2;-2),C(3;0;-4)$ . Viết phương trình trung tuyến đỉnh $A$ của tam giác $ABC$ .

A. $frac{x-2}{1}=frac{y+1}{1}=frac{z}{-3}$ . B. $frac{x-2}{1}=frac{y+1}{-2}=frac{z}{3}$ .

C. $frac{x-2}{1}=frac{y+1}{-2}=frac{z}{-3}$ . D. $frac{x-2}{-1}=frac{y+1}{-2}=frac{z}{3}$ .

Lời giải:

Gọi $M(1;1;-3)$ là trung điểm của cạnh $BC$ , ta có $overrightarrow{AM}=(-1;1;-3)$ là vecto chỉ phương của đường thẳng $AM$ .

Do đó phương trình đường trung tuyến $AM$ là $frac{x-2}{1}=frac{y+1}{-2}=frac{z}{3}$ .

Chọn đáp án B.

Dạng 2. Vị trí tương đối của đường thẳng và mặt phẳng

Ví dụ 2.1 (THPT Chuyên Bắc Giang 2017 Lần 1) Cho đường thẳng $d:frac{x-1}{-1}=frac{y}{2}=frac{z-3}{4}$ và mặt phẳng $(P):2x-y+z-5=0$ . Xét vị trí tương đối của $d$ và $(P)$ .

A. $d$ nằm trên $(P)$ . B. $d$ // $(P)$ .

C. $d$ cắt và không vuông góc với $(P)$ . D. $dbot (P)$ .

Lời giải:

Đường thẳng $d$ đi qua $M(1;0;3)$ và có $VTCP,,,overrightarrow{{{u}_{d}}}(-1;2;4)$ , mặt phẳng $(P)$ có một $VTPT$ $overrightarrow{{{n}_{P}}}(2;-1;1)$ .

Ta có $overrightarrow{{{u}_{d}}}.overrightarrow{{{n}_{P}}}=-1.2+2(-1)+4.1=0$ .

Do đó $d$ song song hoặc nằm trên $(P)$ .

Mặt khác $2.1-0+3-5=0Rightarrow M(1;0;3)in (P)$ .

Vậy $d$ nằm trên $(P)$ . Chọn đáp án A.

Ví dụ 2.2: Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng $d$ có phương trình là $left{ begin{array}{l}x=5-t\y=1+2t\z=-3end{array} right.$ và mặt phẳng $(P)$ có phương trình $-x+2y-2=0$ . Tìm tọa độ giao điểm của mặt phẳng $(P)$ và đường thẳng $d$ .

A. $N(4;3;3)$ . B. $N(4;3;0)$ . C. $N(4;-3;-3)$ . D. $N(4;3;-3)$ .

Mytranshop.com khuyên bạn nên xem: Luật Phạt Góc Trong Bóng Đá Là Gì? 2022 | Mytranshop.com

Lời giải:

Cách 1 (Tự luận)

Xét phương trình $-(5-t)+2(1+2t)-2=0Leftrightarrow 5t-5=0Leftrightarrow t=1$ .

Thay $t=1$ vào phương trình đường thẳng $d$ , ta được tọa độ giao điểm của $d$ và $(P)$ là $N(4,3,-3)$ .

Cách 2 (Trắc nghiệm)

Vì $Nin dRightarrow {{z}_{N}}=-3Rightarrow$ Loại đáp án A và B.

$Nin (P)$ nên thay tọa độ $N$ vào phương trình mặt phẳng $(P)Rightarrow$ Chọn đáp án C.

Ví dụ 2.3: Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng $d$ có phương trình $left{ begin{array}{l}x=2+t\y=-3-t\z=-tend{array} right.$ và điểm $A(1;3;5)$ . Viết phương trình mặt phẳng $(P)$ đi qua điểm $A$ và vuông góc với đường thẳng $d$ .

A. $x-y-z-7=0$ . B. $x-y+z+7=0$ .

C. $x-y-z+7=0$ . D. $x+y-z+7=0$ .

Lời giải:

$overrightarrow{u}(1;-1;-1)$ là $VTCP$ của đường thẳng $d$ .

Vì $(P)bot d$ nên $overrightarrow{u}(1;-1;-1)$ cũng là $VTPT$ của $(P)$ .

Phương trình mặt phẳng $(P)$ đi qua điểm $A(1;3;5)$ và có $VTPT,,(1;-1;-1)$ là:

$x-1-(y-3)-(z-5)=0Leftrightarrow x-y-z+7=0$ .

Chọn đáp án C.

Ví dụ 2.4: Phương trình tham số của đường thẳng $Delta$ đi qua hai điểm $M(1;2;3)$ và vuông góc với mặt phẳng $(P)$ có phương trình $x-4y-5z+3=0$ là

A. $left{ begin{array}{l}x=1+t\y=2-4t\z=3-5tend{array} right.$ . B. $left{ begin{array}{l}x=1+t\y=2+4t\z=3+5tend{array} right.$ . C. $left{ begin{array}{l}x=1+t\y=-2-4t\z=-3-5tend{array} right.$ . D. $left{ begin{array}{l}x=1+t\y=2+4t\z=3-5tend{array} right.$ .

Lời giải:

Ta có $overrightarrow{n}=(1;-4;-5)$ là một vecto pháp tuyến của mặt phẳng $(P)$ .

Vì $Delta bot (P)Rightarrow overrightarrow{n}(1;-4;-5)$ cũng là vecto chỉ phương của đường thẳng $Delta$ .

Vậy phương trình đường thẳng $Delta$ là $left{ begin{array}{l}x=1+t\y=2-4t\z=3-5tend{array} right.$ .

Chọn đáp án A.

Ví dụ 2.5 (Chuyên Bắc Giang 2017 Lần 1) Viết phương trình mặt phẳng vuông góc với mặt phẳng $(alpha ):2x-3y+z-2=0$ và chứa đường thẳng $d:frac{x}{-1}=frac{y+1}{2}=frac{z-2}{-1}$ .

A. $x-y+z-3=0$ . B. $2x+y-z+3=0$ .

C. $x+y+z-1=0$ . D. $3x+y-z+3=0$ .

Lời giải:

Đường thẳng $d$ đi qua điểm $M(0;-1;2)$ và có vecto chỉ phương $overrightarrow{{{u}_{d}}}=(-1;2;-1)$ .

Mặt phẳng $(alpha )$ có vecto pháp tuyến $overrightarrow{n}=(2;-3;1)$ .

Mặt phẳng $(P)$ cần tìm đi qua điểm $M(0;-1;2)$ và có vecto pháp tuyến $left[ overrightarrow{n},overrightarrow{u} right]=(-1;-1;-1)$ có phương trình là $x+y+z-1=0$ . Chọn C.

Dạng 3. Vị trí tương đối của hai đường thẳng. Viết phương trình đường thẳng liên quan đến một đường thẳng

A. Phương pháp

B. Bài tập ví dụ

Ví dụ 3.1 (THPT Chuyên Lê Hồng Phong – Nam Định 2017 Lần 2) Trong không gian với hệ tọa độ $Oxyz$ , cho hai đường thẳng ${{d}_{1}}:frac{x-1}{2}=frac{y-7}{1}=frac{z}{4}$ và ${{d}_{2}}:frac{x+1}{1}=frac{y-2}{2}=frac{z-2}{-1}$ . Mệnh đề nào sau đây là mệnh đề đúng?

A. ${{d}_{1}}$ và ${{d}_{2}}$ vuông góc với nhau và cắt nhau. B. ${{d}_{1}}//{{d}_{2}}$ .

C. ${{d}_{1}}$ và ${{d}_{2}}$ chéo nhau. D. ${{d}_{1}}equiv {{d}_{2}}$ .

Lời giải:

Đường thẳng ${{d}_{1}}:frac{x-1}{2}=frac{y-7}{1}=frac{z}{4}$ có vecto chỉ phương $overrightarrow{{{u}_{1}}}=(2;1;4)$ .

Đường thẳng ${{d}_{2}}:frac{x+1}{1}=frac{y-2}{2}=frac{z-2}{-1}$ có vecto chỉ phương $displaystyle overrightarrow{{{u}_{2}}}=(1;2;-1)$ .

Ta thấy $overrightarrow{{{u}_{1}}}$ và $overrightarrow{{{u}_{2}}}$ không cùng phương nên đáp án B, C sai.

Phương trình tham số ${{d}_{1}}:left{ begin{array}{l}x=1+2t\y=7+t\z=4tend{array} right.,,{{d}_{2}}:left{ begin{array}{l}x=-1+s\y=2+2s\z=2-send{array} right.$ .

Xét hệ $left{ begin{array}{l}1+2t=-1+s\7+t=2+2s\4t=2-send{array} right.Leftrightarrow left{ begin{array}{l}2t-s=-2\t-2s=-5\4t=2-send{array} right.$ $Leftrightarrow left{ begin{array}{l}t=frac{1}{3}\s=frac{8}{3}\4.frac{1}{3}ne 2-frac{8}{3}end{array} right.$ hệ vô nghiệm.

Suy ra ${{d}_{1}}$ và ${{d}_{2}}$ chéo nhau. Chọn đáp án C.

Ví dụ 3.2: Phương trình tham số của đường thẳng $Delta$ đi qua điểm $M(1;2;3)$ và song song với đường thẳng $d$ có phương trình $frac{x-1}{1}=frac{y+3}{-4}=frac{z-1}{-5}$ là

A. $left{ begin{array}{l}x=1+t\y=2-4t\z=3-5tend{array} right.$ . B. $left{ begin{array}{l}x=3+t\y=4t\z=-5tend{array} right.$ . C. $left{ begin{array}{l}x=1+t\y=-2-4t\z=-3-5tend{array} right.$ . D. $left{ begin{array}{l}x=3+t\y=-4t\z=-5tend{array} right.$ .

Lời giải:

Ta có $displaystyle overrightarrow{u}=(1;-4;-5)$ là một vecto chỉ phương của đường thẳng $d$ .

Vì $Delta //dRightarrow overrightarrow{u}(1;-4;-5)$ cũng là một vecto chỉ phương của đường thẳng $Delta$ .

Vậy phương trình của đường thẳng $Delta$ là $left{ begin{array}{l}x=1+t\y=2-4t\z=3-5tend{array} right.$ .

Chọn đáp án A.

Ví dụ 3.3: Trong không gian với hệ tọa độ $Oxyz$ cho điểm $A(2;0;1)$ và đường thẳng $d:frac{x-1}{1}=frac{y}{2}=frac{z-2}{1}$ . Viết phương trình đường thẳng đi qua điểm $A$ , vuông góc và cắt đường thẳng $d$ .

A. $left{ begin{array}{l}x=2-t\y=0\z=2+tend{array} right.$ . B. $left{ begin{array}{l}x=2-t\y=1\z=1+tend{array} right.$ . C. $left{ begin{array}{l}x=2-t\y=0\z=1+tend{array} right.$ . D. $left{ begin{array}{l}x=1-t\y=0\z=1+tend{array} right.$ .

Lời giải:

Gọi $Delta$ là đường thẳng đi qua điểm $A$ , vuông góc và cắt đường thẳng $d$ tại $M$ .

$Rightarrow Min dRightarrow M(1+m;2m;2+m),,,min mathbb{R}$ .

$overrightarrow{u}(1;2;1)$ là vecto chỉ phương của $d$ .

Mytranshop.com khuyên bạn nên xem: Trị mụn bằng oxy già có hiệu quả? Các bước thực hiện tại nhà 2022 | Mytranshop.com

Vì $dbot Delta Leftrightarrow overrightarrow{u}.overrightarrow{AM}=0Leftrightarrow 4m=0Leftrightarrow m=0$ .

Do đó vecto chỉ phương của $Delta$ là $overrightarrow{AM}(-1;0;1)$ .

Phương trình tham số của $Delta$ là $left{ begin{array}{l}x=2-t\y=0\z=1+tend{array} right.$ .

Chọn đáp án C.

Ví dụ 3.4: Trong không gian với hệ tọa độ $Oxyz$ cho mặt phẳng $(P):3x+5y-z-2=0$ và đường thẳng $d:frac{x-12}{4}=frac{y-9}{3}=frac{z-1}{1}$ . Viết phương trình đường thẳng nằm trong mặt phẳng $(P)$ , đi qua giao điểm của $d$ và $(P)$ , đồng thời vuông góc với $d$ ?

A. $frac{x}{8}=frac{y}{-7}=frac{z+2}{-11}$ . B. $frac{x}{8}=frac{y}{-7}=frac{z+2}{-11}$ .

C. $frac{x}{8}=frac{y}{-7}=frac{z+2}{-11}$ . D. $frac{x}{8}=frac{y}{-7}=frac{z+2}{-11}$ .

Lời giải:

Gọi $M$ là giao điểm của $d$ và $(P)Rightarrow M(12+4t;9+3t;1+t)$ .

$Min (P)Rightarrow$ $3(12+4t)+5(9+3t)-(1+t)-2=0Leftrightarrow t=-3$ . Do đó $M(0;0;-2)$ .

$d$ có vecto chỉ phương $overrightarrow{u}=(4;3;1),,(P)$ có vecto chỉ phương $overrightarrow{n}=(3;5;-1)Rightarrow Delta$ có vecto chỉ phương $overrightarrow{v}=left[ overrightarrow{n},overrightarrow{u} right]=(8;-7;-11)$ .

Phương trình đường thẳng $Delta$ là $frac{x}{8}=frac{y}{-7}=frac{z+2}{-11}$ . Chọn đáp án A.

Dạng 4. Viết phương trình đường thẳng liên quan đến hai đường thẳng

A. Phương pháp

B. Bài tập ví dụ

Ví dụ 4.1: Cho hai đường thẳng ${{d}_{1}},{{d}_{2}}$ có phương trình lần lượt là ${{d}_{1}}:left{ begin{array}{l}x={{t}_{1}}\y=-1-4{{t}_{1}}\z=6+6{{t}_{1}}end{array} right.$ và ${{d}_{2}}:frac{x}{2}=frac{y-1}{1}=frac{z+2}{-5}$ . Phương trình của ${{d}_{3}}$ đi qua $M(1;-1;2)$ và vuông góc với cả ${{d}_{1}},{{d}_{2}}$ là

A. $left{ begin{array}{l}x=1-14t\y=-1+17t\z=2+9tend{array} right.$ . B. $left{ begin{array}{l}x=1+14t\y=-1+17t\z=2+9tend{array} right.$ . C. $left{ begin{array}{l}x=1+14t\y=-1-17t\z=2+9tend{array} right.$ . D. $left{ begin{array}{l}x=1+14t\y=-1+17t\z=2-9tend{array} right.$ .

Lời giải:

Vecto chỉ phương của ${{d}_{3}}$ là $overrightarrow{{{u}_{3}}}=left[ overrightarrow{{{u}_{1}}},overrightarrow{{{u}_{2}}} right]=(14;17;9)$ .

Chọn đáp án B.

Ví dụ 4.2 (THPT Chuyên KHTN 2017 Lần 4) Trong không gian với hệ tọa độ $Oxyz$ , cho hai đường thẳng ${{d}_{1}}:frac{x-1}{1}=frac{y-2}{3}=frac{z}{1};,{{d}_{2}}:frac{x+1}{-1}=frac{y-1}{2}=frac{z-2}{4}$ . Đường thẳng $d$ qua $M$ cắt ${{d}_{1}},{{d}_{2}}$ lần lượt tại $A$ và $B$ . Tính độ dài đoạn thẳng $AB$ .

A. $AB=2$ . B. $AB=3$ . C. $AB=sqrt{6}$ . D. $AB=sqrt{5}$ .

Lời giải:

Giả sử $A(1+a;2+3a;a),,,B(-1-b;1+2b;2+4b)$ .

$overrightarrow{MA}=(a-2;3a-1;a+2),,overrightarrow{MB}=(-b-4;2b-2;4b-4)$ .

Ta có $overrightarrow{MA}=koverrightarrow{MB}Leftrightarrow left{ begin{array}{l}a-2=k(-b-4)\3a-1=k(2b-2)\a+2=k(4b-4)end{array} right.$ $Leftrightarrow left{ begin{array}{l}a=0\b=0end{array} right.Rightarrow AB=3$ .

Chọn đáp án B.

Ví dụ 4.3: Trong không gian với hệ tọa độ $Oxyz$ cho điểm $A(1;2;3)$ và đường thẳng $d:frac{x+1}{2}=frac{y}{1}=frac{z-3}{-2}$ . Viết phương trình đường thẳng $Delta$ đi qua điểm $A$ , vuông góc với $d$ và cắt trục $Ox$ .

A. $left{ begin{array}{l}x=1-2t\y=2-2t\z=3+3tend{array} right.$ . B. $left{ begin{array}{l}x=-2t\y=2-2t\z=3-3tend{array} right.$ . C. $left{ begin{array}{l}x=1-2t\y=2-2t\z=3-3tend{array} right.$ . D. $left{ begin{array}{l}x=1-2t\y=2+2t\z=3-3tend{array} right.$ .

Lời giải:

Gọi $B(x;0;0)$ là giao điểm của đường thẳng $Delta$ với trục $Ox$ . Khi đó, đường thẳng $Delta$ nhận vecto $overrightarrow{AB}=(x-1;-2;-3)$ làm vecto pháp tuyến. Vì đường thẳng $Delta$ vuông góc với đường thẳng $d$ nên $overrightarrow{AB}.overrightarrow{{{u}_{d}}}=0Leftrightarrow (x-1).2-2+6=0Leftrightarrow x=-1$ .

Đường thẳng $Delta$ nhận vecto $overrightarrow{AB}=(-2;-2;-3)$ làm vecto pháp tuyến có phương trình $left{ begin{array}{l}x=1-2t\y=2-2t\z=3-3tend{array} right.$ .

Chọn đáp án C.

Ví dụ 4.4: Trong không gian với hệ tọa độ $Oxyz$ , cho ${{d}_{1}}:left{ begin{array}{l}x=3-4{{t}_{1}}\y=-2+{{t}_{1}}\z=-1+{{t}_{1}}end{array} right.$ và ${{d}_{2}}:left{ begin{array}{l}x=6{{t}_{2}}\y=1+{{t}_{2}}\z=2+2{{t}_{2}}end{array} right.$ . Lập phương trình đường vuông góc chung của ${{d}_{1}}$ và ${{d}_{2}}$ .

A. $frac{x-1}{1}=frac{y-1}{2}=frac{z+1}{2}$ . B. $frac{x-1}{1}=frac{y+1}{2}=frac{z-1}{2}$ .

C. $frac{x+1}{1}=frac{y+1}{2}=frac{z}{2}$ . D. $frac{x+1}{1}=frac{y-1}{2}=frac{z}{2}$ .

Lời giải:

Đường thẳng ${{d}_{1}},{{d}_{2}}$ có vecto chỉ phương lần lượt là $overrightarrow{{{u}_{1}}}=(-4;1;1),overrightarrow{{{u}_{2}}}=(-6;1;2)$ .

Giả sử $M=dcap {{d}_{1}}Rightarrow M(3-4{{t}_{1}};-2+{{t}_{1}};-1+{{t}_{1}})$ .

$N=dcap {{d}_{2}}Rightarrow N(-6{{t}_{2}};1+{{t}_{2}};2+2{{t}_{2}})$ .

$Rightarrow overrightarrow{MN}=(-6{{t}_{2}}+4{{t}_{1}}-3;{{t}_{2}}-{{t}_{1}}+3;2{{t}_{2}}-{{t}_{1}}+3)$ .

$MN$ là đoạn vuông góc chung của ${{d}_{1}},{{d}_{2}}$

$Leftrightarrow left{ begin{array}{l}overrightarrow{MN}bot overrightarrow{{{u}_{1}}}\overrightarrow{MN}bot overrightarrow{{{u}_{2}}}end{array} right.Leftrightarrow left{ begin{array}{l}overrightarrow{MN}.overrightarrow{{{u}_{1}}}=0\overrightarrow{MN}.overrightarrow{{{u}_{2}}}=0end{array} right.Leftrightarrow left{ begin{array}{l}3{{t}_{2}}-2{{t}_{1}}+2=0\41{{t}_{2}}-27{{t}_{1}}+27=0end{array} right.$ $Leftrightarrow left{ begin{array}{l}{{t}_{1}}=1\{{t}_{2}}=0end{array} right.Rightarrow M(-1;-1;0),N(0;1;2)$ .

Phương trình đường vuông góc chung của ${{d}_{1}},{{d}_{2}}$ là $frac{x+1}{1}=frac{y+1}{2}=frac{z}{2}$ .

Dạng 5. Khoảng cách – Viết phương trình đường thẳng liên quan đến khoảng cách

Ví dụ 5.1: Trong không gian tọa độ $Oxyz$ , cho hai đường thẳng ${{d}_{1}}:frac{x+7}{3}=frac{y-5}{-1}=frac{z-9}{4}$ và ${{d}_{2}}:frac{x}{3}=frac{y+4}{-1}=frac{z+18}{4}$ . Tính khoảng cách giữa ${{d}_{1}}$ và ${{d}_{2}}$ .

A. $dleft( {{d}_{1}},{{d}_{2}} right)=25$ . B. $dleft( {{d}_{1}},{{d}_{2}} right)=20$ .

C. $dleft( {{d}_{1}},{{d}_{2}} right)=15$ . D. $dleft( {{d}_{1}},{{d}_{2}} right)=sqrt{15}$ .

Lời giải:

Ta thấy ${{d}_{1}}$ và ${{d}_{2}}$ là hai đường thẳng song song, nên ta chỉ việc lấy một điểm bất kì thuộc ${{d}_{1}}$ và tính khoảng cách từ điểm đó đến ${{d}_{2}}$ .

Gọi $M(-7;5;8)in {{d}_{1}},,H(0;-4;-18)in {{d}_{2}}$

Ta có: $overrightarrow{MH}=(7;-9;-27)$ .

Vecto chỉ phương của ${{d}_{2}}$ là $overrightarrow{{{u}_{{{d}_{2}}}}}=(3;-1;4)Rightarrow left[ overrightarrow{MH},overrightarrow{{{u}_{{{d}_{2}}}}} right]=(-63;-109;20)$ .

Vậy $dleft( {{d}_{1}},{{d}_{2}} right)=dleft( M,{{d}_{2}} right)=frac{left| overrightarrow{MH},overrightarrow{{{u}_{{{d}_{2}}}}} right|}{left| overrightarrow{{{u}_{{{d}_{2}}}}} right|}=25$ .

Ví dụ 5.2: Trong không gian với hệ tọa độ $Oxyz$ , tính khoảng cách $d$ từ điểm $A(1;-2;3)$ đến đường thẳng $d:frac{x-10}{5}=frac{y-2}{1}=frac{z+2}{1}$ .

A. $d=sqrt{frac{1361}{27}}$ . B. $d=7$ . C. $d=frac{13}{2}$ . D. $d=sqrt{frac{1358}{27}}$ .

Lời giải:

Đường thẳng $d$ có vecto chỉ phương $overrightarrow{u}=(5;1;1)$ . Gọi điểm $M(10;2;-2)in d$ .

Mytranshop.com khuyên bạn nên xem: ĐÁ TỰ NHIÊN LÀ GÌ??? | Kiến Thức Xây Dựng 2022 | Mytranshop.com

Ta có $displaystyle overrightarrow{AM}=(9;4;-5)Rightarrow left[ overrightarrow{AM},overrightarrow{u} right]=(9;-34;-11)$ .

$dleft( A,d right)=frac{left| left[ overrightarrow{AM},overrightarrow{u} right] right|}{left| overrightarrow{u} right|}=sqrt{frac{1358}{27}}$ .

Chọn đáp án D.

Ví dụ 5.2: Trong không gian với hệ tọa độ $Oxyz$ , cho mặt phẳng $(P):2x+y-2z+9=0$ và đường thẳng $d:frac{x+1}{1}=frac{y-1}{7}=frac{z-3}{-1}$ . Viết phương trình đường thẳng $Delta$ vuông góc với $(P)$ và cắt $d$ tại một điểm $M$ cách $(P)$ một khoảng bằng 2.

A. $left{ begin{array}{l}x=-frac{19}{11}+2t\y=-frac{45}{11}+t\z=frac{41}{11}-2tend{array} right.$ . B. $left{ begin{array}{l}x=-frac{7}{11}+2t\y=frac{39}{11}+t\z=frac{29}{11}-2tend{array} right.$ .

C. $left{ begin{array}{l}x=-frac{7}{11}+2t\y=frac{39}{11}-t\z=frac{29}{11}-2tend{array} right.$ . D. Cả A, B đều đúng.

Lời giải:

Vì $Delta bot (P)Rightarrow overrightarrow{{{n}_{P}}}(2;1;-2)$ là một vecto chỉ phương của $Delta$ .

Giả sử $Delta cap d=MRightarrow M(t-1;1+7t;3-t)$ .

Ta có $dleft( M,(P) right)=2Leftrightarrow |11t+2|,=6Leftrightarrow left[ begin{array}{l}t=-frac{8}{11}\t=frac{4}{11}end{array} right.$ .

Với $t=-frac{8}{11}Rightarrow Mleft( -frac{19}{11};-frac{45}{11};frac{41}{11} right)$ .

Với $t=frac{4}{11}Rightarrow Mleft( -frac{7}{11};frac{39}{11};frac{29}{11} right)Rightarrow Delta :left{ begin{array}{l}x=-frac{7}{11}+2t\y=frac{39}{11}+t\z=frac{29}{11}-2tend{array} right.$ $Rightarrow Delta :left{ begin{array}{l}x=-frac{19}{11}+2t\y=-frac{45}{11}+t\z=frac{41}{11}-2tend{array} right.$ .

Ví dụ 5.2: Trong không gian với hệ tọa độ $Oxyz$ , cho mặt phẳng $(P):x-2y+2z-5=0$ và các điểm $A(-3;0;1),B(1;-1;3)$ . Trong tất cả các đường thẳng đi qua $A$ và song song với mặt phẳng $(P)$ , gọi $d$ là đường thẳng sao cho khoảng cách từ $B$ đến $d$ là lớn nhất. Viết phương trình đường thẳng $d$ .

A. $frac{x-5}{2}=frac{y}{-6}=frac{z}{-7}$ . B. $frac{x-1}{-2}=frac{y+12}{6}=frac{z+13}{7}$ .

C. $frac{x+3}{-2}=frac{y}{-6}=frac{z-1}{7}$ . D. $frac{x-1}{-2}=frac{y+1}{6}=frac{z-3}{7}$ .

Lời giải:

Vì $(-3-2.0+2.1-5)(1-2.(-1)+2.3-5)<0$ nên hai điểm $A,B$ khác phía so với $(P)$ . Gọi $H$ là hình chiếu của $B$ lên $d$ .

Ta có $BHle BA$ nên khoảng cách $BH$ từ $B$ đến $d$ lớn nhất khi và chỉ khi $Hequiv A$ .

Khi đó $ABbot d$ .

Vecto pháp tuyến của $(P)$ là $overrightarrow{n}=(1;-2;2)$ .

$overrightarrow{AB}=(4;-1;2)$ .

Vecto chỉ phương của $d$ là $overrightarrow{u}=left[ overrightarrow{u},overrightarrow{AB} right]=(-2;6;7)$ .

Mà $d$ qua $A(-3;0;1)$ nên chọn B.

Dạng 6. Góc giữa hai đường thẳng – Góc giữa đường thẳng và mặt phẳng.

A. Phương pháp

B. Bài tập ví dụ

Ví dụ 6.1: Trong không gian với hệ tọa độ $Oxyz$ , số đo của góc tạo bởi hai đường thẳng ${{d}_{1}}:left{ begin{array}{l}x=-1+t\y=2\z=2+tend{array} right.$ và ${{d}_{2}}:left{ begin{array}{l}x=8-2t'\y=t'\z=2t'end{array} right.$ là

A. ${{90}^{0}}$ . B. ${{60}^{0}}$ . C. ${{30}^{0}}$ . D. ${{45}^{0}}$ .

Lời giải:

Vecto chỉ phương của ${{d}_{1}}$ là $overrightarrow{{{u}_{1}}}=(1;0;1)$ .

Vecto chỉ phương của ${{d}_{2}}$ là $overrightarrow{{{u}_{2}}}=(-2;1;2)$ .

Ta có $overrightarrow{{{u}_{1}}}.overrightarrow{{{u}_{2}}}=0Rightarrow {{d}_{1}}bot {{d}_{2}}$

Vậy góc tạo bởi ${{d}_{1}}$ và ${{d}_{2}}$ là ${{90}^{0}}$ .

Chọn A.

Ví dụ 6.2: Trong không gian với hệ tọa độ $Oxyz$ , cho hai đường thẳng ${{d}_{1}}:left{ begin{array}{l}x=-1+t\y=sqrt{2}t\z=2+tend{array} right.$ và ${{d}_{2}}:left{ begin{array}{l}x=2+t\y=1+sqrt{2}t\z=2+mtend{array} right.$ . Với giá trị nào của m thì ${{d}_{1}}$ và ${{d}_{2}}$ hợp với nhau một góc ${{60}^{0}}$ ?

A. $m=-1$ . B. $m=1$ . C. $m=frac{1}{2}$ . D. $m=-frac{3}{2}$ .

Lời giải:

Vecto chỉ phương của ${{d}_{1}}$ là $overrightarrow{{{u}_{1}}}=(1;sqrt{2};1)$ .

Vecto chỉ phương của ${{d}_{2}}$ là $overrightarrow{{{u}_{2}}}=(1;sqrt{2};m)$ .

Ta có $displaystyle cos {{60}^{0}}=left| cos (overrightarrow{{{u}_{1}}},overrightarrow{{{u}_{2}}}) right|Leftrightarrow |m+3|,=sqrt{{{m}^{2}}+3}Leftrightarrow m=-1$

Chọn A.

Ví dụ 6.3: Trong không gian với hệ tọa độ $Oxyz$ , cho đường thẳng $d:left{ begin{array}{l}x=1-t\y=2+t\z=tend{array} right.$ và mặt phẳng $(P):2x+3y+z-4=0$ . Tính $sin left( d,(P) right)$ .

A. $frac{-sqrt{42}}{21}$ . B. $frac{sqrt{42}}{21}$ . C. $frac{sqrt{21}}{42}$ . D. $frac{-sqrt{21}}{42}$ .

Lời giải:

Vecto chỉ phương của đường thẳng d là $overrightarrow{u}=(-1;1;0)$ .

Vecto pháp tuyến của mặt phẳng $(P)$ là $overrightarrow{n}=(2;3;1)$ .

Ta có $sin left( d,(P) right)=frac{left| overrightarrow{u}.overrightarrow{n} right|}{left| overrightarrow{u} right|.left| overrightarrow{n} right|}=frac{sqrt{42}}{21}$ .

Chọn B.

Ví dụ 6.4: Trong không gian với hệ tọa độ $Oxyz$ , cho hai đường thẳng $d,d'$ có phương trình $d:left{ begin{array}{l}x=1+t\y=2+t\z=tend{array} right.,,,,d':left{ begin{array}{l}x=1\y=1+sqrt{2}t'\z=sqrt{2}t'end{array} right.$ . Viết phương trình đường thẳng $Delta$ đi qua điểm A(3; 2; 2), vuông góc với đường thẳng d và tạo với đường thẳng d’ một góc ${{60}^{0}}$ .

A. $left{ begin{array}{l}x=3+t\y=2\z=2-tend{array} right.,,left{ begin{array}{l}x=3+t\y=2\z=2-tend{array} right.$ . B. $left{ begin{array}{l}x=3-t\y=2\z=2-tend{array} right.,,left{ begin{array}{l}x=3+t\y=2\z=2-tend{array} right.$ .

C. $left{ begin{array}{l}x=3+t\y=2\z=2+tend{array} right.,,left{ begin{array}{l}x=3+t\y=2\z=2-tend{array} right.$ . D. $left{ begin{array}{l}x=3+t\y=2\z=2+tend{array} right.,,left{ begin{array}{l}x=3+t\y=2\z=2+tend{array} right.$ .

Lời giải:

Đường thẳng d có vecto chỉ phương $overrightarrow{u}=(1;-1;1)$ .

Đường thẳng d’ có vecto chỉ phương $overrightarrow{u'}=(0;sqrt{2};sqrt{2})$ .

Gọi $overrightarrow{v}=(a;b;c),,({{a}^{2}}+{{b}^{2}}+{{c}^{2}}>0)$ là một vecto chỉ phương của đường thẳng $Delta$ .

Ta có $overrightarrow{u}bot overrightarrow{v}Leftrightarrow overrightarrow{u}.overrightarrow{v}=0Leftrightarrow a+b+c=0Leftrightarrow a=-b-c$ .

$cos (Delta ,d')=frac{left| sqrt{2}b+sqrt{2}c right|}{2sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$ $Rightarrow frac{left| sqrt{2}b+sqrt{2}c right|}{2sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=frac{1}{2}Leftrightarrow left[ begin{array}{l}b=0\c=0end{array} right.$ .