A. Lý thuyết cơ bản
1. Phương trình mặt cầu
Dạng tổng quát: Mặt cầu có tâm
và bán kính
có phương trình:
.
Dạng khai triển:
(*).
(*) là phương trình của một mặt cầu .
Khi đó có tâm
và bán kính
.
2. Vị trí tương đối giữa mặt phẳng và mặt cầu 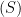
Mặt cầu có tâm
, bán kính
và mặt phẳng
.
+ : mặt phẳng
và mặt cầu
không cắt nhau.
+ : mặt phẳng
tiếp xúc với mặt cầu
.
được gọi tiếp diện của mặt cầu
. Khi đó
là một
của
.
+ : mặt phẳng
cắt mặt cầu
theo một đường tròn
có tâm và bán kính được xác định như sau:
– Tâm : là hình chiếu của
trên
.
– Bán kính .

3. Vị trí tương đối giữa đường thẳng và mặt cầu
Cho đường thẳng và mặt cầu
có tâm
, bán kính
.
+ : đường thẳng
và mặt cầu
không cắt nhau.
+ : đường thẳng
tiếp xúc với mặt cầu
tại
. Khi đó
được gọi là tiếp tuyến của
.
+ : đường thẳng
cắt mặt cầu
tại 2 điểm
phân biệt (
được gọi là cát tuyến của
).

B. Bài tập
Dạng 1. Xác định tâm, bán kính của mặt cầu. Tìm điều kiện để phương trình dạng khai triển là phương trình của một đường tròn
A. Phương pháp
+ tâm
và bán kính
.
+ (*) là phương trình của một mặt cầu
.
Khi đó có tâm
và bán kính
.
B. Bài tập ví dụ
Ví dụ 1.1: Cho mặt cầu . Tìm tâm
, bán kính
của mặt cầu
.
A. . B.
.
C. . D.
.
Lời giải:
Chọn đáp án A.
Ví dụ 1.2: Cho mặt cầu . Tìm tọa độ tâm
, bán kính
của mặt cầu
.
A. . B.
.
C. . D.
.
Lời giải:
.
có tâm
và bán kính
.
Chọn đáp án C.
Ví dụ 1.3: Tìm tất cả các giá trị thực của tham số để phương trình
là phương trình của một mặt cầu.
A. hoặc
. B.
.
C. hoặc
. D.
.
Lời giải:
Ta có .
Đề phương trình trên là phương trình mặt cầu thì
Chọn đáp án A.
Dạng 2. Viết phương trình mặt cầu có tâm  và bán kính
và bán kính 
A. Phương pháp
Mặt cầu có tâm
và bán kính
có phương trình
.
Do đó, muốn viết được phương trình của mặt cầu thì cần phải xác định được tâm và bán kính
.
Chú ý:
– Mặt cầu có đường kính
và tâm
là trung điểm của
.
– Mặt cầu tâm đi qua điểm
.
– Viết phương trình mặt cầu đi qua 4 điểm
:
+ Giả sử .
+ Vì nên ta có hệ gồm 4 phương trình, 4 ẩn. Giải hệ này tìm được tâm và bán kính của
.
B. Bài tập ví dụ
Ví dụ 2.1: Viết phương trình mặt cầu có tâm
đi qua
.
A. .
B. .
C. .
D. .
Lời giải:
Mặt cầu có bán kính .
Vậy phương trình mặt cầu là .
Vậy chọn đáp án D.
Ví dụ 2.2: Trong không gian với hệ tọa độ , cho hai điểm
. Phương trình nào dưới đây là phương trình của mặt cầu đường kính
?
A. . B.
.
C. . D.
.
Lời giải:
Gọi là tâm mặt cầu đường kính
suy ra
là trung điểm của
nên
.
Mà .
Vậy .
Chọn đáp án A.
Ví dụ 2.3 (Chuyên KHTN 2017 Lần 4) Trong không gian với hệ tọa độ , cho ba điểm
. Tính bán kính
của mặt cầu đi qua bốn điểm
.
A. . B.
. C.
. D.
.
Lời giải:
Phương trình mặt cầu có dạng với
.
Theo giả thiết ta có hệ phương trình:
.
Chọn đáp án A.
Ví dụ 2.4: Trong không gian với hệ tọa độ , cho hình lăng trụ tam giác
có
và
. Viết phương trình mặt cầu đi qua bốn điểm
?
A. . B.
.
C. . D.
.
Lời giải:
Phương trình mặt cầu có dạng với
.
Theo giả thiết ta có hệ phương trình .
Vậy phương trình mặt cầu cần tìm là .
Chọn đáp án C.
Ví dụ 2.5: Trong không gian với hệ tọa độ , cho điểm
và mặt phẳng
. Mặt cầu
có tâm
nằm trên mặt phẳng
, đi qua điểm
và gốc tọa độ
sao cho chu vi tam giác
bằng
. Phương trình mặt cầu
là
A. hoặc
.
B. hoặc
.
C. hoặc
.
D. hoặc
.
Lời giải:
Gọi là tâm của mặt cầu
.
Khi đó nên ta suy ra hệ
.
Giải hệ ta tìm được hoặc
.
Chọn đáp án D.
Dạng 3. Vị trí tương đối của mặt phẳng và mặt cầu
Ví dụ 3.1: Cho mặt phẳng và mặt cầu
. Mệnh đề nào sau đây là mệnh đề sai ?
A. cắt
theo một đường tròn. B.
tiếp xúc với
.
C. có điểm chung với
. D.
đi qua tâm của
.
Lời giải:
Mặt cầu tâm
và có bán kính
.
.
Vậy tiếp xúc với
.
Chọn đáp án B.
Ví dụ 3.2: Cho mặt cầu và mặt phẳng
. Tìm tất cả các giá trị thực của
để
và
tiếp xúc với nhau.
A. . B.
.
C. . D.
.
Lời giải:
có tâm
và bán kính
.
Để và
tiếp xúc với nhau thì
.
Chọn đáp án A.
Ví dụ 3.3: Cho mặt cầu và mặt phẳng
. Tìm tất cả các giá trị thực của
để
và
có điểm chung.
A. . B.
.
C. . D.
.
Lời giải:
Mặt cầu có tâm
và bán kính
.
Để và
cắt nhau thì:
.
Chọn đáp án B.
Ví dụ 3.4: Trong không gian với hệ tọa độ , cho điểm
và mặt phẳng
. Viết phương trình mặt cầu
có tâm
và tiếp xúc với mặt phẳng
.
A. . B.
.
C. . D.
.
Lời giải:
Bán kính mặt cầu là .
Phương trình của mặt cầu là . Chọn đáp án B.
Ví dụ 3.5: Trong không gian với hệ tọa độ , cho điểm
và mặt phẳng
. Phương trình mặt cầu
. Viết phương trình của mặt phẳng
song song với mặt phẳng
và tiếp xúc với mặt cầu
.
A. . B.
.
C. . D.
.
Lời giải:
Vì có dạng
.
Mặt phẳng tiếp xúc với
nên
(vì
).
Vậy phương trình của mặt phẳng là
.
Chọn đáp án A.
Ví dụ 3.6: Trong không gian với hệ tọa độ , cho mặt phẳng
và mặt cầu
. Tìm tọa độ tâm của đường tròn giao tuyến của mặt phẳng
và mặt cầu
.
A. . B.
. C.
. D.
.
Lời giải:
Tâm của đường tròn giao tuyến là hình chiếu vuông góc của
lên
.
Đường thẳng qua
và vuông góc với
có phương trình
.
Do .
Ta có .
Vậy . Chọn đáp án D.
Ví dụ 3.7: Trong không gian , cho mặt cầu
. Viết phương trình mặt phẳng
đi qua điểm
cắt mặt cầu
theo đường tròn có bán kính nhỏ nhất.
A. . B.
. C.
. D.
.
Lời giải:

Mặt cầu có tâm
và bán kính
.
Ta có .
Do đó, mặt phẳng qua
luôn cắt mặt cầu
theo một đường tròn.
Gọi là bán kính của đường tròn và
là hình chiếu vuông góc của
lên mặt phẳng
.
Vì vuông tại
.
Đẳng thức xảy ra .
Khi đó là vecto pháp tuyến của mặt phẳng
.
.
Chọn đáp án B.
Ví dụ 3.8: Trong không gian với hệ tọa độ , cho mặt cầu
có phương trình
và mặt phẳng
. Viết phương trình mặt phẳng
song song với
và cắt
theo giao tuyến là đường tròn có chu vi bằng
.
A. . B.
.
C. . D. Cả A và B.
Lời giải:
Do nên
có phương trình
.
có tâm
, bán kính
. Đường tròn giao tuyến có chu vi bằng
nên có bán kính
.
Khoảng cách từ đến
là
.
Do đó .
Vậy có phương trình
.
Ví dụ 3.9: Trong không gian với hệ tọa độ , cho biết
là tập hợp tâm của các mặt cầu
đi qua điểm
đồng thời tiếp xúc với hai mặt phẳng
và
. Diện tích hình phẳng giới hạn bởi đường cong
là
A. . B.
. C. 3. D.
.
Lời giải:
Gọi là tâm của mặt cầu
. Theo đề bài ta có
.
.
.
Vậy tập hợp tâm của mặt cầu
là giao tuyến của mặt cầu
và mặt phẳng
hay chính là đường tròn có bán kính
.
Vậy diện tích của hình phẳng cần tìm là .
Ví dụ 3.10 (Đề minh họa lần 2 năm 2017) Trong không gian với hệ tọa độ , xét các điểm
và
với
và
. Biết rằng khi
thay đổi, tồn tại một mặt cầu cố định tiếp xúc với mặt phẳng
và đi qua
. Tính bán kính
của mặt cầu đó?
A. . B.
. C.
. D.
.
Lời giải:
Gọi và
là bán tâm và bán kính của mặt cầu cố định trong đề bài.
Ta có
Phương trình là
.
.
Vì nên
.
Do đó .
Ta xét hai trường hợp:
TH1: Nếu thì thay
vào, ta có
Đăng thức này đúng với mọi nên
hay
thay vào (*) thì
hay
.
TH2: Nếu thì tương tự trên, ta có
hay
.
Suy ra hay
(không thỏa mãn).
Vậy mặt cầu cần tìm là .
Nhận xét:
Với cách giải trên, ta thấy rằng nếu không cho điểm , ta vẫn có thể tìm được liên hệ giữa tọa độ tam và bán kính của mặt cầu cố định cần tìm. Việc đưa thêm điểm
vào giúp ta có thể giải phương trình tìm
.
Dạng 4. Vị trí tương đối của đường thẳng và mặt cầu
Ví dụ 4.1: Trong không gian với hệ tọa độ , cho đường thẳng
:
và mặt cầu
:
. Mệnh đề nào dưới đây là đúng?
A. và
cắt nhau tại hai điểm.
B. tiếp xúc với
.
C. và
không có điểm chung.
D. Tất cả các đáp án trên đều sai.
Lời giải:
Đường thẳng có vecto chỉ phương
và đi qua điểm
.
Chuyển về dạng tham số
.
Mặt cầu có tâm
và bán kính
.
Xét phương trình (vô nghiệm)
Vậy và
không có điểm chung.
Chọn đáp án C.
Ví dụ 4.2: Trong không gian với hệ tọa độ , viết phương trình mặt cầu
có tâm
và tiếp xúc với đường thẳng
.
A. . B.
.
C. . D.
.
Lời giải:
Mặt cầu có tâm
và bán kính
.
Đường thẳng đi qua
và có
.
tiếp xúc với đường thẳng
.
.
Chọn đáp án B.
Ví dụ 4.3: Trong không gian với hệ tọa độ , cho điểm
và đường thẳng
. Viết phương trình mặt cầu
có tâm là điểm
và cắt tại hai điểm phân biệt
sao cho đoạn thẳng
có độ dài bẳng 4.
A. . B.
.
C. . D.
.
Lời giải:

Giả sử mặt cầu cắt
tại hai điểm
sao cho
có bán kính
.
Gọi là trung điểm đoạn
.
Khi đó vuông tại
.
Ta có .
.
Vậy phương trình của mặt cầu cần tìm là
.
Vậy chọn đáp án C.
Ví dụ 4.4: Trong không gian với hệ tọa độ , cho đường thẳng
và điểm
. Viết phương trình mặt cầu tâm
. Viết phương trình mặt cầu tâm
và tiếp xúc với đường thẳng
.
A. . B.
.
C. . D.
.
Lời giải:
Gọi . Khi đó
.
Do đó phương trình mặt cầu cần tìm là .
Chọn đáp án A.
Ví dụ 4.5: Trong không gian với hệ tọa độ , cho mặt cầu
và đường thẳng
. Tìm
để đường thẳng
cắt
tại hai điểm
sao cho độ dài đoạn
.
A. . B.
. C.
. D.
.
Lời giải:
có tâm
và bán kính
.
Gọi là trung điểm của
.
Đường thẳng qua
và có vecto chỉ phương
.
Suy ra .
Ta có .
Chọn đáp án D.