Phương trình lượng giác thường gặp, trắc nghiệm toán học lớp 11 2022

I. Phương trình bậc nhất đối với một hàm số lượng giác

A. Phương pháp

Định nghĩa: Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:

$at+b=0$ trong đó $a,b$ là các hằng số $(ane 0)$ và $t$ là một hàm số lượng giác.
Cách giải: Chuyển vế rồi chia hai vế của phương trình cho $a$ , đưa về phương trình lượng giác cơ bản.

B. Bài tập ví dụ

Ví dụ 1: Gọi $S$ là tập nghiệm của phương trình $2cos x-sqrt{3}=0$ . Khẳng định nào sau đây là đúng?

A. $frac{5pi }{6}in S$ . B. $frac{11pi }{6}in S$ . C. $frac{13pi }{6}notin S$ . D. $-frac{13pi }{6}notin S$ .

Lời giải:

Ta có $2cos x-sqrt{3}=0Leftrightarrow cos x=cos frac{pi }{6}$ .

$Leftrightarrow x=pm frac{pi }{6}+k2pi ,(kin mathbb{Z})$

Ta thấy với họ nghiệm $x=-frac{pi }{6}+k2pi$ , thay $k=1$ ta được $frac{11pi }{6}in S$ .

Chọn B.

Ví dụ 2: Số vị trí điểm biểu diễn các nghiệm của phương trình $tan left( 2x-frac{pi }{3} right)+sqrt{3}=0$ trên đường tròn lượng giác là?

A. 4. B. 3. C. 2. D. 1.

Lời giải:

Ta có $displaystyle tan left( 2x-frac{pi }{3} right)+sqrt{3}=0Leftrightarrow tan left( 2x-frac{pi }{3} right)=-sqrt{3}$

$displaystyle Leftrightarrow tan left( 2x-frac{pi }{3} right)=tan left( -frac{pi }{3} right)$

$Leftrightarrow 2x-frac{pi }{3}=-frac{pi }{3}+kpi Leftrightarrow x=frac{kpi }{2},(kin mathbb{Z})$ .

Do đó có 4 điểm biểu diễn nghiệm của phương trình đã cho trên đường tròn lượng giác là $A,B,C,D$ .

Chọn A.

Ví dụ 3: Phương trình $(sin x+1)(sin x-sqrt{2})=0$ có nghiệm là

A. $x=-frac{pi }{2}+k2pi ,(kin mathbb{Z})$ . B. $x=pm frac{pi }{4}+k2pi ;-frac{pi }{8}+kpi ,(kin mathbb{Z})$ .

C. $x=frac{pi }{2}+k2pi$ . D. $x=pm frac{pi }{2}+k2pi$ .

Lời giải:

$(sin x+1)(sin x-sqrt{2})=0Leftrightarrow left[ begin{array}{l}sin x=-1\sin x=sqrt{2}end{array} right.$ .

$Leftrightarrow x=-frac{pi }{2}+k2pi ,(kin mathbb{Z})$

Chọn A.

Ví dụ 4: Nghiệm của phương trình ${{sin }^{4}}x-{{cos }^{4}}x=0$ là

A. $x=-frac{pi }{4}+kpi$ . B. $x=frac{pi }{4}+kfrac{pi }{2}$ . C. $x=frac{3pi }{4}+k2pi$ . D. $x=pm frac{pi }{4}+k2pi$ .

Lời giải:

${{sin }^{4}}x-{{cos }^{4}}x=0Leftrightarrow ({{sin }^{2}}x+{{cos }^{2}}x)({{sin }^{2}}-{{cos }^{2}}x)=0$

$Leftrightarrow {{sin }^{2}}-{{cos }^{2}}x=0Leftrightarrow {{cos }^{2}}x-{{sin }^{2}}x=0Leftrightarrow cos 2x=0$

$Leftrightarrow 2x=frac{pi }{2}+kpi Leftrightarrow x=frac{pi }{4}+kfrac{pi }{2},(kin mathbb{Z})$

Chọn B.

Ví dụ 5: Giải phương trình $4({{sin }^{6}}x+{{cos }^{6}}x)+2({{sin }^{4}}x+{{cos }^{4}}x)=8-4{{cos }^{2}}2x$ .

A. $x=pm frac{pi }{3}+frac{kpi }{2},,kin mathbb{Z}$ . B. $x=pm frac{pi }{24}+frac{kpi }{2},,kin mathbb{Z}$ .

C. $x=pm frac{pi }{12}+frac{kpi }{2},,kin mathbb{Z}$ . D. $x=pm frac{pi }{6}+frac{kpi }{2},,kin mathbb{Z}$ .

Lời giải:

Ta có:

$4({{cos }^{6}}x+{{sin }^{6}}x)+2({{sin }^{4}}x+{{cos }^{4}}x)=8-4{{cos }^{2}}2x$

$begin{array}{l}Leftrightarrow 4left[ {{({{sin }^{2}}x+{{cos }^{2}}x)}^{3}}-3{{sin }^{2}}x{{cos }^{2}}x({{sin }^{2}}x+{{cos }^{2}}) right]\+2left[ {{({{sin }^{2}}x+{{cos }^{2}}x)}^{2}}-2{{sin }^{2}}x{{cos }^{2}}x right]end{array}$

$=8-4{{cos }^{2}}2x$

$Leftrightarrow 4(1-3{{sin }^{2}}x{{cos }^{2}}x)+2(1-2{{sin }^{2}}x{{cos }^{2}}x)=8-4{{cos }^{2}}2x$

$Leftrightarrow 6-16{{sin }^{2}}x{{cos }^{2}}x=8-4{{cos }^{2}}2x$

$Leftrightarrow 6-4{{sin }^{2}}2x=8-4{{cos }^{2}}2x$

$Leftrightarrow 4{{cos }^{2}}2x-4{{sin }^{2}}2x=2Leftrightarrow 4cos 4x=2$

$Leftrightarrow cos 4x=frac{1}{2}Leftrightarrow x=pm frac{pi }{12}+frac{kpi }{2},,kin mathbb{Z}$

Chọn C.

Ví dụ 6: Phương trình $frac{sin 3x}{cos 2x}+frac{cos 3x}{sin 2x}=frac{2}{sin 3x}$ có nghiệm là

A. $x=frac{pi }{8}+kfrac{pi }{4}$ . B. $x=frac{pi }{6}+kfrac{pi }{3}$ . C. $x=frac{pi }{3}+kfrac{pi }{2}$ . D. $x=frac{pi }{4}+kpi$ .

Lời giải:

Điều kiện: $left{ begin{array}{l}cos 2xne 0\sin 2xne 0\sin 3xne 0end{array} right.Leftrightarrow left{ begin{array}{l}2xne frac{kpi }{2}\3xne kpi end{array} right.$ $Leftrightarrow left{ begin{array}{l}xne frac{kpi }{4}\xne frac{kpi }{3}end{array} right.$

Phương trình tương đương: $frac{sin 3x.sin 2x+cos 2x.cos 3x}{sin 2x.cos 2x}=frac{2}{sin 3x}$

$Leftrightarrow frac{2cos x}{sin 4x}=frac{2}{sin 3x}Leftrightarrow sin 3x.cos x=sin 4x$

$Leftrightarrow frac{1}{2}(sin 2x+sin 4x)=sin 4x$

$Leftrightarrow sin 2x=sin 4xLeftrightarrow left[ begin{array}{l}2x=4x+k2pi \2x=pi -4x+k2pi end{array} right.$ .

$Leftrightarrow left[ begin{array}{l}x=-kpi \x=frac{pi }{6}+frac{kpi }{3}end{array} right.$

Mytranshop.com khuyên bạn nên xem: Công thức tính lực ma sát trượt | Kiến Thức Xây Dựng 2022 | Mytranshop.com

Kết hợp với điều kiện ta được nghiệm $x=frac{pi }{6}+kfrac{pi }{3}$ .

Chọn B.

II. Phương trình bậc nhất đối với 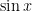$sin x$ và $cos x$

A. Phương pháp

Định nghĩa: Phương trình bậc nhất đối với $sin x$ và $displaystyle cos x$ là phương trình có dạng:

$displaystyle asin x+bcos x=c$
Cách giải: Điều kiện để phương trình có nghiệm: ${{a}^{2}}+{{b}^{2}}ge {{c}^{2}}$ .

Chia hai vế của phương trình cho $sqrt{{{a}^{2}}+{{b}^{2}}}$ ta được:

$displaystyle frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}sin x+frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}}cos x=frac{c}{sqrt{{{a}^{2}}+{{b}^{2}}}}$

Do $displaystyle {{left( frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}+{{left( frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}} right)}^{2}}=1$ nên đặt $left{ begin{array}{l}frac{a}{sqrt{{{a}^{2}}+{{b}^{2}}}}=cos alpha \frac{b}{sqrt{{{a}^{2}}+{{b}^{2}}}}=sin alpha end{array} right.$ .

Khi đó phương trình trở thành:

$cos alpha .sin x+sin alpha .cos x=frac{c}{sqrt{{{a}^{2}}+{{b}^{2}}}}$ . $Leftrightarrow sin (x+alpha )=frac{c}{sqrt{{{a}^{2}}+{{b}^{2}}}}$

B. Bài tập ví dụ

Ví dụ 1: Cho phương trình $msin x-sqrt{1-3m}cos x=m-2$ . Tìm tất cả các giá trị thực của $m$ để phương trình có nghiệm.

A. $frac{1}{3}le mle 3$ . B. $mle frac{1}{3}$ . C. $min varnothing$ . D. $mge 3$ .

Lời giải:

$sqrt{1-3m}$ có nghĩa $Leftrightarrow 1-3mge 0Leftrightarrow mle frac{1}{3}$ (1)

Phương trình có nghiệm $Leftrightarrow {{m}^{2}}+{{left( -sqrt{1-3m} right)}^{2}}ge {{(m-2)}^{2}}Leftrightarrow mge 3$ (2)

Từ (1), (2) suy ra không có giá trị nào của $m$ để phương trình có nghiệm.

Ví dụ 2: Nghiệm của phương trình $sin 2x-sqrt{3}cos 2x=0$ là

A. $x=frac{pi }{3}+kfrac{pi }{2},,kin mathbb{Z}$ . B. $x=frac{pi }{6}+kpi ,,kin mathbb{Z}$ .

C. $x=frac{pi }{3}+kpi ,,kin mathbb{Z}$ . D. $x=frac{pi }{6}+kfrac{pi }{2},,kin mathbb{Z}$ .

Lời giải:

$sin 2x-sqrt{3}cos 2x=0Leftrightarrow frac{1}{2}sin 2x-frac{sqrt{3}}{2}cos 2x=0$

$Leftrightarrow cos frac{pi }{3}.sin 2x-sin frac{pi }{3}.cos 2x=0Leftrightarrow -sin left( frac{pi }{3}-2x right)=0$

$Leftrightarrow frac{pi }{3}-2x=kpi Leftrightarrow x=frac{pi }{6}+kfrac{pi }{2},(kin mathbb{Z})$

Chọn D.

Ví dụ 3: Phương trình nào sau đây vô nghiệm:

A. $2sin x-cos x=-3$ . B. $sin x=frac{sqrt{3}}{2}$ .

C. $sqrt{3}sin 2x-cos 2x=2$ . D. $3sin x-4cos x=5$ .

Lời giải:

Dựa vào điều kiện có nghiệm của phương trình $asin x+bcos x=c$ là ${{a}^{2}}+{{b}^{2}}ge {{c}^{2}}$ .

Chọn A.

Ví dụ 4: Số nghiệm của phương trình $sin x+cos x=1$ trên khoảng $(0;pi )$ là

A. 0. B. 1. C. 2. D. 3.

Lời giải:

$sin x+cos x=1Leftrightarrow sqrt{2}sin left( x+frac{pi }{4} right)=1$ $Leftrightarrow sin left( x+frac{pi }{4} right)=frac{sqrt{2}}{2}$

$Leftrightarrow left[ begin{array}{l}x+frac{pi }{4}=frac{pi }{4}+k2pi \x+frac{pi }{4}=frac{3pi }{4}+k2pi end{array} right.Leftrightarrow left[ begin{array}{l}x=frac{pi }{2}+k2pi \x=k2pi end{array} right.(kin mathbb{Z})$

Trên khoảng $(0;pi )$ phương trình có một nghiệm là $x=frac{pi }{2}$ .

Chọn B.

Ví dụ 5: Giải phương trình $frac{cos x-2sin xcos x}{2{{cos }^{2}}x+sin x-1}=sqrt{3}$ .

A. $x=frac{5pi }{18}+frac{kpi }{3},kin mathbb{Z}$ . B. $x=frac{5pi }{18}+frac{k2pi }{3},kin mathbb{Z}$ .

C. $x=frac{5pi }{18}+frac{k4pi }{3},kin mathbb{Z}$ . D. $x=frac{5pi }{18}+frac{k5pi }{3},kin mathbb{Z}$ .

Lời giải:

Điều kiện: $2{{cos }^{2}}x+sin x-1ne 0Leftrightarrow 1-2{{sin }^{2}}x+sin x-1ne 0$

$Leftrightarrow 2{{sin }^{2}}x-sin xne 0Leftrightarrow left{ begin{array}{l}sin xne 0\sin xne frac{1}{2}end{array} right.$ .

Phương trình $Leftrightarrow cos x-sin 2x=sqrt{3}left[ (2{{cos }^{2}}x-1)+sin x right]$

$Leftrightarrow cos x-sin 2x=sqrt{3}(cos 2x+sin x)$

$Leftrightarrow cos x-sqrt{3}sin x=sqrt{3}cos 2x+sin 2x$

$Leftrightarrow sin left( 2x+frac{pi }{3} right)=sin left( x-frac{pi }{6} right)$

$Leftrightarrow left[ begin{array}{l}x=-frac{pi }{2}+k2pi \x=frac{5pi }{18}+frac{k2pi }{3}end{array} right.(kin mathbb{Z})$

Kết hợp với điều kiện ta được nghiệm $x=frac{5pi }{18}+frac{k2pi }{3},kin mathbb{Z}$ .

Chọn B.

Ví dụ 6: Giải phương trình $4({{sin }^{4}}x+{{cos }^{4}}x)+sqrt{3}sin 4x=2$ .

A. $left[ begin{array}{l}x=frac{pi }{4}+frac{kpi }{7}\x=-frac{pi }{12}+frac{kpi }{7}end{array} right.(kin mathbb{Z})$ . B. $left[ begin{array}{l}x=frac{pi }{4}+frac{kpi }{5}\x=-frac{pi }{12}+frac{kpi }{5}end{array} right.(kin mathbb{Z})$ .

C. $left[ begin{array}{l}x=frac{pi }{4}+frac{kpi }{3}\x=-frac{pi }{12}+frac{kpi }{3}end{array} right.(kin mathbb{Z})$ . D. $left[ begin{array}{l}x=frac{pi }{4}+frac{kpi }{2}\x=-frac{pi }{12}+frac{kpi }{2}end{array} right.(kin mathbb{Z})$ .

Lời giải:

Phương trình $Leftrightarrow 4left[ {{({{sin }^{2}}x+{{cos }^{2}}x)}^{2}}-2{{sin }^{2}}x{{cos }^{2}}x right]+sqrt{3}sin 4x=2$

$Leftrightarrow 4left( 1-frac{1}{2}{{sin }^{2}}2x right)+sqrt{3}sin 4x-2=0$

$Leftrightarrow 2-2{{sin }^{2}}2x+sqrt{3}sin 4x=0$

$Leftrightarrow 2-(1-cos 4x)+sqrt{3}sin 4x=0$

$Leftrightarrow cos 4x+sqrt{3}sin 4x=-1$

$Leftrightarrow frac{1}{2}cos 4x+frac{sqrt{3}}{2}sin 4x=-frac{1}{2}$

$Leftrightarrow cos left( 4x-frac{pi }{3} right)=cos frac{2pi }{3}$

$Leftrightarrow left[ begin{array}{l}x=frac{pi }{4}+frac{kpi }{2}\x=-frac{pi }{12}+frac{kpi }{2}end{array} right.(kin mathbb{Z})$

Chọn D.

III. Phương trình bậc hai đối với một hàm số lượng giác

A. Phương pháp

Định nghĩa: Phương trình bậc hai đối với một hàm số lượng giác là phương trình có dạng:

$a{{t}^{2}}+bt+c=0$ trong đó $a,b,c$ là các hằng số $(ane 0)$ và $t$ là một hàm số lượng giác.
Cách giải: Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện cho ẩn phụ (nếu có) rồi giải phương trình bậc hai theo ẩn phụ này. Cuối cùng đưa về giải các phương trình lượng giác cơ bản.

B. Bài tập ví dụ

Ví dụ 1: Nghiệm của phương trình $2{{sin }^{2}}x-3sin x+1=0$ thuộc khoảng $displaystyle left[ 0;frac{pi }{2} right)$ là?

Mytranshop.com khuyên bạn nên xem: Tác hại của việc uống nước ngọt quá nhiều 2022 | Mytranshop.com

A. $x=frac{pi }{3}$ . B. $x=frac{pi }{2}$ . C. $x=frac{pi }{6}$ . D. $x=frac{5pi }{6}$ .

Lời giải:

Đặt $t=sin x,,(-1le tle 1)$ , phương trình trở thành: $2{{t}^{2}}-3t+1=0Leftrightarrow left[ begin{array}{l}t=1\t=frac{1}{2}end{array} right.$ .

Với $t=1$ ta có: $sin x=1Leftrightarrow x=frac{pi }{2}+k2pi ,(kin mathbb{Z})$ .

Do $0le x<frac{pi }{2}$ nên $0le frac{pi }{2}+k2pi <frac{pi }{2}Leftrightarrow frac{-1}{4}le k<0$ . Vì $kin mathbb{Z}$ nên không tồn tại $k$ .
Với $t=frac{1}{2}$ ta có: $sin x=frac{1}{2}Leftrightarrow left[ begin{array}{l}x=frac{pi }{6}+k2pi \x=frac{5pi }{6}+k2pi end{array} right.$ .

Do $0le x<frac{pi }{2}$ nên $x=frac{pi }{6}$ .

Chọn C.

Ví dụ 2: Phương trình $sqrt{3}tan x+cot x-sqrt{3}-1=0$ có nghiệm là

A. $left[ begin{array}{l}x=frac{pi }{4}+kpi \x=frac{pi }{6}+kfrac{pi }{2}end{array} right.(kin mathbb{Z})$ . B. $left[ begin{array}{l}x=frac{pi }{4}+k2pi \x=frac{pi }{6}+k2pi end{array} right.(kin mathbb{Z})$ .

C. $left[ begin{array}{l}x=frac{pi }{4}+k3pi \x=frac{pi }{6}+k3pi end{array} right.(kin mathbb{Z})$ . D. $left[ begin{array}{l}x=frac{pi }{4}+kpi \x=frac{pi }{6}+kpi end{array} right.(kin mathbb{Z})$ .

Lời giải:

Điều kiện: $left{ begin{array}{l}sin xne 0\cos xne 0end{array} right.Leftrightarrow sin 2xne 0$ (*)

Phương trình $Leftrightarrow sqrt{3}tan x+frac{1}{tan x}-sqrt{3}-1=0$

$Leftrightarrow sqrt{3}{{tan }^{2}}x-(sqrt{3}+1)tan x+1=0$

$Leftrightarrow left[ begin{array}{l}tan x=1\tan x=frac{1}{sqrt{3}}end{array} right.Leftrightarrow left[ begin{array}{l}x=frac{pi }{4}+kpi \x=frac{pi }{6}+kpi end{array} right.$ (thỏa mãn điều kiện (*))

Chọn D.

Ví dụ 3: Phương trình $3cos 4x+2cos 2x-5=0$ có nghiệm là

A. $k2pi$ . B. $frac{pi }{3}+k2pi$ . C. $kpi$ . D. $-frac{pi }{3}+k2pi$ .

Lời giải:

Phương trình $Leftrightarrow 3(2{{cos }^{2}}2x-1)+2cos 2x-5=0$

$Leftrightarrow 6{{cos }^{2}}2x+2cos 2x-8=0$

$Leftrightarrow left[ begin{array}{l}cos 2x=1\cos 2x=-frac{4}{3}end{array} right.Rightarrow cos 2x=1$ .

$Leftrightarrow 2x=k2pi Leftrightarrow x=kpi ,,kin mathbb{Z}$

Chọn C.

Ví dụ 4: Tìm tất cả các giá trị thực của tham số $m$ để phương trình $cos 2x-(2m+1)cos x+m+1=0$ có nghiệm trên khoảng $left( frac{pi }{2};frac{3pi }{2} right)$ ?

A. $-1le mle 0$ . B. $-1le m<0$ . C. $-1<m<0$ . D. $-1le m<frac{1}{2}$ .

Lời giải:

Phương trình $Leftrightarrow 2{{cos }^{2}}x-(2m+1)cos x+m=0$ .

$Leftrightarrow left[ begin{array}{l}cos x=frac{1}{2}\cos x=mend{array} right.$

Nhận thấy phương trình $cos x=frac{1}{2}$ không có nghiệm trên khoảng $left( frac{pi }{2};frac{3pi }{2} right)$ . Do đó phương trình đã cho có nghiệm thuộc khoảng $left( frac{pi }{2};frac{3pi }{2} right)$ khi và chỉ khi phương trình $cos x=m$ có nghiệm thuộc $left( frac{pi }{2};frac{3pi }{2} right)$ $Leftrightarrow -1le m<0$ .

Chọn B.

IV. Phương trình đẳng cấp bậc hai đối với 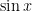$sin x$ và $cos x$

A. Phương pháp

Định nghĩa: Phương trình bậc hai đối với $sin x$ và $cos x$ là phương trình có dạng:

$displaystyle a{{sin }^{2}}x+bsin xcos x+c{{cos }^{2}}x=0$

Cách giải:
- + Kiểm tra xem $cos x=0Leftrightarrow x=frac{pi }{2}+kpi$ có là nghiệm của phương trình không.
- + Khi $cos xne 0Leftrightarrow xne frac{pi }{2}+kpi$ , chia hai vế của phương trình cho ${{cos }^{2}}x$ ta thu được phương trình: $displaystyle a{{tan }^{2}}x+btan x+c=0$
  
  Đây là phương trình bậc hai đối với $tan x$ mà ta đã biết cách giải.

Chú ý:
- + Phương trình dạng $displaystyle a{{sin }^{2}}x+bsin xcos x+c{{cos }^{2}}x=d$ ta làm như sau:
- + Đối với phương trình đẳng cấp bậc ba: $displaystyle a{{sin }^{3}}x+b{{sin }^{2}}xcos x+csin x{{cos }^{2}}x+d{{cos }^{3}}x=0$
  
  thì cách giải cũng hoàn toàn tương tự như trên.

B. Bài tập ví dụ

Ví dụ 1: Cho phương trình ${{cos }^{2}}x-3sin xcos x+1=0$ . Mệnh đề nào sau đây là sai?

A. $x=kpi$ không là nghiệm của phương trình.

B. Nếu chia hai vế của phương trình cho ${{cos }^{2}}x$ thì ta được phương trình ${{tan }^{2}}x-3tan x+2=0$ .

C. Nếu chia 2 vế của phương trình cho ${{sin }^{2}}x$ thì ta được phương trình $2{{cot }^{2}}x+3cot x+1=0$ .

D. Phương trình đã cho tương đương với $cos 2x-3sin 2x+3=0$ .

Lời giải:

Với $x=kpi Rightarrow left{ begin{array}{l}sin x=0\cos x=pm 1end{array} right.Leftrightarrow left{ begin{array}{l}sin x=0\{{cos }^{2}}x=1end{array} right.$ . Thay vào phương trình ta thấy thỏa mãn. Vậy A đúng.
Chia cả hai vế của phương trình cho ${{cos }^{2}}x$ ta được:

$frac{{{cos }^{2}}x}{{{cos }^{2}}x}-frac{3sin xcos x}{{{cos }^{2}}x}+frac{1}{{{cos }^{2}}x}=0$ $Leftrightarrow 1-frac{3sin x}{cos x}+(1+{{tan }^{2}}x)=0$

$Leftrightarrow {{tan }^{2}}x-3tan x+2=0$

Vậy B đúng.
Chia cả hai vế của phương trình cho ${{sin }^{2}}x$ ta được:

$frac{{{cos }^{2}}x}{{{sin }^{2}}x}-frac{3sin xcos x}{{{sin }^{2}}x}+frac{1}{{{sin }^{2}}x}=0$ $Leftrightarrow {{cot }^{2}}x-frac{3cos x}{sin x}+(1+{{cot }^{2}}x)=0$

$Leftrightarrow 2{{cot }^{2}}x-3cot x+1=0$

Vậy C sai.
Phương trình $Leftrightarrow frac{1+cos 2x}{2}-frac{3}{2}sin 2x+1=0$ .

$Leftrightarrow cos 2x-3sin 2x+3=0$

Vậy D đúng.

Chọn C.

Ví dụ 2: Phương trình ${{sin }^{2}}x-4sin xcos x+4{{cos }^{2}}x=5$ tương đương với phương trình nào sau đây?

A. $cos x=0$ . B. $cot x=1$ . C. $tan x=frac{1}{2}$ . D. $tan x=-frac{1}{2}$ .

Mytranshop.com khuyên bạn nên xem: 5 mẫu mặt bằng nhà vườn cấp 4 đẹp nên tham khảo trước khi xây nhà 2022 | Mytranshop.com

Lời giải:

Xét $cos x=0Rightarrow sin x=pm 1Rightarrow {{sin }^{2}}x=1$ , thay vào phương trình ta được: $1=5$ (vô lí).

Do đó $x=frac{pi }{2}+kpi$ không là nghiệm của phương trình.
Với $xne frac{pi }{2}+kpi$ , chia cả hai vế của phương trình cho ${{cos }^{2}}x$ ta được:

$frac{{{sin }^{2}}x}{{{cos }^{2}}x}-frac{4sin xcos x}{{{cos }^{2}}x}+frac{4{{cos }^{2}}x}{{{cos }^{2}}x}=frac{5}{{{cos }^{2}}x}$

$Leftrightarrow {{tan }^{2}}x-4tan x+4-5(1+{{tan }^{2}}x)=0$

$Leftrightarrow 4{{tan }^{2}}x+4tan x+1=0Leftrightarrow {{(2tan x+1)}^{2}}=0$

$Leftrightarrow tan x=-frac{1}{2}Leftrightarrow x=-arctan frac{1}{2}+kpi$

Chọn D.

Ví dụ 3: Số nghiệm của phương trình ${{cos }^{2}}x-3sin xcos x+2{{sin }^{2}}x=0$ trên khoảng $(-2pi ;2pi )$ là

A. 2. B. 4. C. 6. D. 8.

Lời giải:

Xét $cos x=0Rightarrow sin x=pm 1Rightarrow {{sin }^{2}}x=1$ , thay vào phương trình ta được: $2=0$ (vô lí). Do đó $x=frac{pi }{2}+kpi$ không là nghiệm của phương trình.
Xét $xne frac{pi }{2}+kpi$ , chia cả hai vế của phương trình cho ${{cos }^{2}}x$ ta được:

$1-3tan x+2{{tan }^{2}}x=0Leftrightarrow left[ begin{array}{l}tan x=1\tan x=frac{1}{2}end{array} right.$ $Leftrightarrow left[ begin{array}{l}x=frac{pi }{4}+kpi \x=arctan frac{1}{2}+kpi end{array} right.(kin mathbb{Z})$

+ Với $x=frac{pi }{4}+kpi$ :

Vì $xin (-2pi ;2pi )Rightarrow -2pi <frac{pi }{4}+kpi <2pi$ $Leftrightarrow -frac{9}{4}<k<frac{7}{4}Rightarrow kin text{ }!!{!!text{ }-2;-1;0;1}$
+ Với $x=arctan frac{1}{2}+kpi$ :

Vì $xin (-2pi ;2pi )Rightarrow -2pi <arctan frac{1}{2}+kpi <2pi$

$Rightarrow -28,565<k<-24,565$

$Rightarrow kin text{ }!!{!!text{ }-28;-27;-26;-25}$ .

Vậy có tất cả 8 nghiệm.

Chọn D.

Ví dụ 4: Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình sau có nghiệm:

${{sin }^{2}}x-2(m-1)sin xcos x-(m-1){{cos }^{2}}x=m$

A. 2. B. 1. C. 0. D. Vô số.

Lời giải:

Xét $cos x=0Rightarrow sin x=pm 1Rightarrow {{sin }^{2}}x=1$ , thay vào phương trình ta được: $1=m$ . Phương trình có nghiệm khi và chỉ khi $m=1$ .
Xét $xne frac{pi }{2}+kpi$ , chia cả hai vế của phương trình cho ${{cos }^{2}}x$ ta được:

$begin{array}{l}{{tan }^{2}}x-2(m-1)tan x-(m-1)=m(1+{{tan }^{2}}x)\Leftrightarrow (1-m){{tan }^{2}}x-2(m-1)tan x-(2m-1)=0,,,,,,,(*)end{array}$

Nếu $m-1=0Leftrightarrow m=1$ ta có: $-1=0$ (vô lí).
Nếu $mne 1$ , phương trình (*) có nghiệm $Leftrightarrow Delta 'ge 0Leftrightarrow -{{m}^{2}}+mge 0Leftrightarrow 0le m<1$ .

Vậy $0le mle 1$ thì phương trình đã cho có nghiệm. Do đó có 2 giá trị nguyên của $m$ thỏa mãn yêu cầu bài.

Cách 2:

Phương trình $(1-m).frac{1-cos 2x}{2}-(m-1)sin 2x-(2m-1).frac{1+cos 2x}{2}=0$

$Leftrightarrow 2(m-1)sin 2x+mcos 2x=2-3m$

Phương trình có nghiệm $Leftrightarrow 4{{(m-1)}^{2}}+{{m}^{2}}ge {{(2-3m)}^{2}}$

$Leftrightarrow 4{{m}^{2}}-4mle 0Leftrightarrow 0le mle 1$

Chọn A.

V. Phương trình chứa 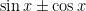$sin xpm cos x$ và $sin xcos x$

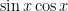
A. Phương pháp

Định nghĩa: Là phương trình có dạng: $a(sin xpm cos x)+bsin xcos x+c=0$
Cách giải: Đặt $t=sin xpm cos x$ (điều kiện $-sqrt{2}le tle sqrt{2}$ ). Biểu diễn $sin xcos x$ theo $t$ ta được phương trình cơ bản.

B. Bài tập ví dụ

Ví dụ 1: Cho $x$ thỏa mãn phương trình $sin 2x+sin x-cos x=1$ . Tính $sin left( x-frac{pi }{4} right)$ .

A. $sin left( x-frac{pi }{4} right)=0$ hoặc $sin left( x-frac{pi }{4} right)=1$ .

B. $sin left( x-frac{pi }{4} right)=0$ hoặc $sin left( x-frac{pi }{4} right)=frac{sqrt{2}}{2}$ .

C. $sin left( x-frac{pi }{4} right)=0$ hoặc $sin left( x-frac{pi }{4} right)=-frac{sqrt{2}}{2}$ .

D. $sin left( x-frac{pi }{4} right)=-frac{sqrt{2}}{2}$ .

Lời giải:

Đặt $displaystyle t=sin x-cos x=sqrt{2}sin left( x-frac{pi }{4} right),,-sqrt{2}le tle sqrt{2}$ .

Ta có ${{t}^{2}}={{(sin x-cos x)}^{2}}=1-2sin xcos x$ $Rightarrow sin xcos x=1-{{t}^{2}}$

Phương trình trở thành: $1-{{t}^{2}}+t=1Leftrightarrow {{t}^{2}}-t=0Leftrightarrow left[ begin{array}{l}t=0\t=1end{array} right.$ .

Với $t=1$ , ta được $sqrt{2}sin left( x-frac{pi }{4} right)=1Leftrightarrow sin left( x-frac{pi }{4} right)=frac{sqrt{2}}{2}$ .

Với $t=0$ , ta được $sqrt{2}sin left( x-frac{pi }{4} right)=0Leftrightarrow sin left( x-frac{pi }{4} right)=0$ .

Chọn B.

Ví dụ 2: Phương trình $(1+sin x)(1+cos x)=2$ có nghiệm là

A. $left[ begin{array}{l}x=frac{pi }{2}+k2pi \x=kpi end{array} right.(kin mathbb{Z})$ . B. $left[ begin{array}{l}x=frac{pi }{4}+kpi \x=kpi end{array} right.(kin mathbb{Z})$ .

C. $left[ begin{array}{l}x=frac{pi }{2}+k2pi \x=k2pi end{array} right.(kin mathbb{Z})$ . D. $left[ begin{array}{l}x=frac{pi }{3}+k2pi \x=k2pi end{array} right.(kin mathbb{Z})$ .

Lời giải:

Phương trình $Leftrightarrow sin x+cos x+sin xcos x-1=0$ .

Đặt $t=sin x+cos x=sqrt{2}cos left( x-frac{pi }{4} right),,tin left[ -sqrt{2};sqrt{2} right]$ .

$Rightarrow {{t}^{2}}=1+2sin xcos xRightarrow sin xcos x=frac{{{t}^{2}}-1}{2}$ .

Phương trình trở thành: $t+frac{{{t}^{2}}-1}{2}-1=0$

$Leftrightarrow {{t}^{2}}+2t-3=0Leftrightarrow t=1$

Với $t=1$ ta có:

$sqrt{2}cos left( x-frac{pi }{4} right)=1Leftrightarrow left[ begin{array}{l}x-frac{pi }{4}=frac{pi }{4}+k2pi \x-frac{pi }{4}=-frac{pi }{4}+k2pi end{array} right.$ $Leftrightarrow left[ begin{array}{l}x=frac{pi }{2}+k2pi \x=k2pi end{array} right.(kin mathbb{Z})$

Chọn D.

Ví dụ 3: Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình sau có nghiệm:

$sin xcos x-sin x-cos x+m=0$

A. 1. B. 2. C. 3. D. 4.

Lời giải:

Đặt $t=sin x+cos x=sqrt{2}cos left( x-frac{pi }{4} right),,tin left[ -sqrt{2};sqrt{2} right]$ .

$Rightarrow {{t}^{2}}=1+2sin xcos xRightarrow sin xcos x=frac{{{t}^{2}}-1}{2}$ .

Phương trình trở thành: $frac{{{t}^{2}}-1}{2}-t+m=0$

$Leftrightarrow {{t}^{2}}-2t+2m-1=0Leftrightarrow {{(t-1)}^{2}}=-2m+2$

Vì $-sqrt{2}le tle sqrt{2}$ $Leftrightarrow -sqrt{2}-1le t-1le sqrt{2}-1Leftrightarrow 0le {{(t-1)}^{2}}le 3+2sqrt{2}$

Do đó phương trình có nghiệm $0le -2m+2le 3+2sqrt{2}$ $Leftrightarrow -frac{1+2sqrt{2}}{2}le mle 1$

$min mathbb{Z}Rightarrow min text{ }!!{!!text{ }-1;0;1}$ .

Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài.

Chọn C.

Phương trình lượng giác thường gặp, trắc nghiệm toán học lớp 11 2022 | Mytranshop.com

I. Phương trình bậc nhất đối với một hàm số lượng giác

A. Phương pháp

B. Bài tập ví dụ

II. Phương trình bậc nhất đối với $sin x$ và $cos x$

A. Phương pháp

B. Bài tập ví dụ

III. Phương trình bậc hai đối với một hàm số lượng giác

A. Phương pháp

B. Bài tập ví dụ

IV. Phương trình đẳng cấp bậc hai đối với $sin x$ và $cos x$

A. Phương pháp

B. Bài tập ví dụ

V. Phương trình chứa $sin xpm cos x$ và $sin xcos x$

A. Phương pháp

B. Bài tập ví dụ

Leave a Comment Cancel reply

I. Phương trình bậc nhất đối với một hàm số lượng giác

A. Phương pháp

B. Bài tập ví dụ

II. Phương trình bậc nhất đối với và

A. Phương pháp

B. Bài tập ví dụ

III. Phương trình bậc hai đối với một hàm số lượng giác

A. Phương pháp

B. Bài tập ví dụ

IV. Phương trình đẳng cấp bậc hai đối với và

A. Phương pháp

B. Bài tập ví dụ

V. Phương trình chứa và

A. Phương pháp

B. Bài tập ví dụ

Leave a Comment Cancel reply

II. Phương trình bậc nhất đối với $sin x$ và $cos x$

IV. Phương trình đẳng cấp bậc hai đối với $sin x$ và $cos x$

V. Phương trình chứa $sin xpm cos x$ và $sin xcos x$