Quy tắc đếm, trắc nghiệm toán học lớp 11 2022 | Mytranshop.com

by

 

A. Lí thuyết cơ bản

 

1. Quy tắc cộng

Định nghĩa: Một công việc nào đó có thể được thực hiện theo một trong hai phương án A hoặc B.
Nếu phương án A có m cách thực hiện, phương án B có n cách thực hiện và không trùng với bất kì cách nào trong phương án A thì công việc đó có m + n cách thực hiện.

Công thức quy tắc cộng

Nếu các tập {{A}_{1}},{{A}_{2}},...,{{A}_{n}} đôi một rời nhau. Khi đó:

left| {{A}_{1}}cup {{A}_{2}}cup ...cup {{A}_{n}} right|=left| {{A}_{1}} right|+left| {{A}_{2}} right|+...+left| {{A}_{n}} right|

2. Quy tắc nhân

Định nghĩa:
Một công việc nào đó có thể bao gồm hai công đoạn A và B. Nếu công đoạn A có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn B thì công việc đó có m.n cách thực hiện.

Công thức quy tắc nhân:

Nếu các tập {{A}_{1}},{{A}_{2}},...,{{A}_{n}} đôi một rời nhau. Khi đó:

left| {{A}_{1}}cap {{A}_{2}}cap ...cap {{A}_{n}} right|=left| {{A}_{1}} right|.left| {{A}_{2}} right|.....left| {{A}_{n}} right|.

B. Bài tập

 

Dạng 1. Sử dụng các quy tắc để thực hiện bài toán đếm số phương án thực hiện hành động H thỏa mãn tính chất T

A. Phương pháp

Cách 1: Đếm trực tiếp

bullet  Nhận xét đề bài để phân chia các trường hợp xảy ra đối với bài toán cần đếm.

bullet  Đếm số phương án thực hiện trong mỗi trường hợp đó

bullet  Kết quả của bài toán là tổng số phương án đếm trong cách trường hợp trên

Cách 2: Đếm gián tiếp (đếm phần bù)

Trong trường hợp hành động H chia nhiều trường hợp thì ta đi đếm phần bù của bài toán như sau:

bullet  Đếm số phương án thực hiện hành động H (không cần quan tâm đến có thỏa tính chất T hay không) ta được aphương án.

bullet  Đếm số phương án thực hiện hành động H không thỏa tính chất T ta được b phương án.

Khi đó số phương án thỏa yêu cầu bài toán là: a-b.

B. Bài tập ví dụ

Ví dụ 1: Một lớp học có displaystyle 25 học sinh nam và displaystyle 20 học sinh nữ. Giáo viên chủ nhiệm muốn chọn ra:

    a) một học sinh đi dự trại hè của trường.

    b) một học sinh nam và một học sinh nữ dự trại hè của trường.

Số cách chọn trong mỗi trường hợp a) và b) lần lượt là:

    A. displaystyle 45 và displaystyle 500 .     B. displaystyle 500 và displaystyle 45.     C. displaystyle 25 và displaystyle 500.     D. displaystyle 500 và displaystyle 25.

Lời giải:

Chọn A.

    a) 

    Bước 1: Với bài toán a thì ta thấy cô giáo có thể có hai phương án để chọn học sinh đi thi:

    Bước 2: Đếm số cách chọn.

  • Phương án 1: chọn 1 học sinh nam đi dự trại hè của trường thì có 25 cách chọn.
  • Phương án 2: chọn 1 học sinh nữ đi dự trại hè của trường thì có 20 cách chọn.
Mytranshop.com khuyên bạn nên xem:  50 ý tưởng thiết kế phòng ngủ nhỏ đẹp, hiện đại và phong cách 2022 | Mytranshop.com

    Bước 3: Áp dụng quy tắc cộng.

    Vậy có 20+25=45 cách chọn.

    b)
    Bước 1: Với bài toán b thì ta thấy công việc là chọn một học sinh nam và một học sinh nữ.

    Do vậy ta có 2 công đoạn.

    Bước 2: Đếm số cách chọn trong các công đoạn.

  • Công đoạn 1: Chọn 1 học sinh nam trong số 25 học sinh nam thì có 25 cách chọn.
  • Công đoạn 2: Chọn 1 học sinh nữ trong số 20 học sinh nữ thì có 20 cách chọn.

    Bước 3: Áp dụng quy tắc nhân.

    Vậy ta có 25.20=500 cách chọn.

CHÚ Ý

  • Quy tắc cộng: Áp dụng khi công việc có nhiều phương án giải quyết.
  • Quy tắc nhân: Áp dụng khi công việc có nhiều công đoạn.

Ví dụ 2: Trên giá sách có 10 quyển sách Văn khác nhau, 8 quyển sách Toán khác nhau và 6 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn nhau?

    A. 80.                    B. 60.                     C. 48.                   D. 188.

Lời giải:

Chọn D.

Theo quy tắc nhân ta có:

10.8=80 cách chọn một quyển sách Văn và một quyển sách Toán khác nhau.

10.6=60 cách chọn một quyển sách Văn và một quyển sách Tiếng Anh khác nhau.

8.6=48 cách chọn một quyển sách Toán và một quyển sách Tiếng Anh khác nhau.

Theo quy tắc cộng ta có số cách chọn 2 quyển sách khác môn là 80+60+48=188 cách.

Nhận xét:

Ta thấy bài toán ở bài toán 2 là sự kết hợp của cả quy tắc cộng và quy tắc nhân khi bài toán vừa

cần chia trường hợp vừa cần lựa chọn theo bước.

Ví dụ 3: Có 3 nam và 3 nữ cần xếp ngồi vào một hàng ghế. Hỏi có mấy cách xếp sao cho: 

a) Nam, nữ ngồi xen kẽ ?

    A. 72                     B. 74                       C. 76                      D. 78

b) Nam, nữ ngồi xen kẽ và có một người nam A, một người nữ B phải ngồi kề nhau ?

    A. 40                     B. 42                       C. 46                      D. 70

c) Nam, nữ ngồi xen kẽ và có một người nam C, một người nữ D không được ngồi kề nhau ?

    A. 32                     B. 30                       C. 35                      D. 70

Mytranshop.com khuyên bạn nên xem:  Điêu khắc chân mày là gì? Nên chọn điêu khắc hay phun xăm chân mày 2022 | Mytranshop.com

Lời giải:

a) Có 6 cách chọn một người tuỳ ý ngồi vào chỗ thứ nhất. Tiếp đến, có 3 cách chọn một người khác phái ngồi vào chỗ thứ 2. Lại có 2 cách chọn một người khác phái ngồi vào chỗ thứ 3, có 2 cách chọn vào chỗ thứ 4, có 1 cách chọn vào chỗ thứ 5, có 1 cách chọn vào chỗ thứ 6.

Vậy có : 6.3.2.2.1.1=72 cách.

Chú ý: Sai lầm có thể mắc phải:

Xếp trước 3 bạn nữ, ta được 3! cách xếp. Cố định mỗi cách sắp các bạn nữ thì ta thấy có 4 vị trí có thể xếp 3 bạn học sinh nam (gồm 2 chỗ giữa các bạn nữ và 2 chỗ đầu hàng, cuối hàng), có A_{4}^{3} cách xếp như vậy. Do đó có 3!.A_{4}^{3} cách xếp.

Đây là lời giải sai do ta đã tính luôn 2 trường hợp sau:

  • Nam – Nữ – Nữ – Nam – Nữ – Nam: TH này có {{left( 3! right)}^{2}}=36 cách
  • Nam – Nữ – Nam – Nữ – Nữ – Nam: TH này cũng có {{left( 3! right)}^{2}}=36 cách

Hai TH này không thỏa mãn yêu cầu đề bài là nam nữ xen kẽ nên lời giải này sai.

b) Cho cặp nam nữ A, B đó ngồi vào chỗ thứ nhất và chỗ thứ hai, có 2 cách. Tiếp đến, chỗ thứ ba có 2 cách chọn, chỗ thứ tư có 2 cách chọn, chỗ thứ năm có 1 cách chọn, chỗ thứ sáu có 1 cách chọn.

Bây giờ, cho cặp nam nữ A, B đó ngồi vào chỗ thứ hai và chỗ thứ ba. Khi đó, chỗ thứ nhất có 2 cách chọn, chỗ thứ tư có 2 cách chọn, chỗ thứ năm có 1 cách chọn, chỗ thứ sáu có 1 cách chọn.

Tương tự khi cặp nam nữ A, B đó ngồi vào chỗ thứ ba và thứ tư, thứ tư và thứ năm, thứ năm và thứ sáu.

Vậy có: 5.2.2.2.1.1.=40 cách.

c) Số cách chọn để cặp nam nữ đó không ngồi kề nhau bằng số cách chọn tuỳ ý trừ số cách chọn để cặp nam nữ đó ngồi kề nhau.

Vậy có : 72-40=32 cách

Dạng 2. Sử dụng các quy tắc để thực hiện bài toán đếm số các số được hình thành từ tập 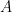A

A. Phương pháp

Khi lập một số tự nhiên x=overline{{{a}_{1}}...{{a}_{n}}} ta cần lưu ý:

* {{a}_{i}}in left{ 0,1,2,...,9 right} và {{a}_{1}}ne 0.

* x là số chẵn Leftrightarrow {{a}_{n}} là số chẵn

* x là số lẻ Leftrightarrow {{a}_{n}} là số lẻ

* x chia hết cho 3Leftrightarrow {{a}_{1}}+{{a}_{2}}+...+{{a}_{n}} chia hết cho 3

* x chia hết cho 4 Leftrightarrow overline{{{a}_{n-1}}{{a}_{n}}} chia hết cho 4

* x chia hết cho 5Leftrightarrow {{a}_{n}}in left{ 0,5 right}

* x chia hết cho 6 Leftrightarrow x là số chẵn và chia hết cho 3

* x chia hết cho 8Leftrightarrow overline{{{a}_{n-2}}{{a}_{n-1}}{{a}_{n}}} chia hết cho 8

* x chia hết cho 9Leftrightarrow {{a}_{1}}+{{a}_{2}}+...+{{a}_{n}} chia hết cho 9.

* x chia hết cho 11Leftrightarrow tổng các chữ số ở hàng lẻ trừ đi tổng các chữ số ở hàng chẵn là một số chia hết cho 11.

* x chia hết cho 25Leftrightarrow  hai chữ số tận cùng là 00,25,50,75.

B. Bài tập ví dụ

Ví dụ 1: Có bao nhiêu chữ số chẵn gồm bốn chữ số đôi một khác nhau được lập từ các số displaystyle 0,1,2,4,5,6,8.

Lời giải:

Gọi x=overline{abcd};text{ }a,b,c,din left{ 0,1,2,4,5,6,8 right}.

Cách 1: Tính trực tiếp

Mytranshop.com khuyên bạn nên xem:  Mạch điện sao tam giác dùng 2 contactor tối ưu về rơ le thời gian

Vì x là số chẵn nên din left{ 0,2,4,6,8 right}.

TH 1: d=0Rightarrow  có 1 cách chọn d.

Với mỗi cách chọn d ta có 6 cách chọn ain left{ 1,2,4,5,6,8 right}

Với mỗi cách chọn a,d ta có 5 cách chọn bin left{ 1,2,4,5,6,8 right}backslash left{ a right}

Với mỗi cách chọn a,b,d ta có 4 cách chọn cin left{ 1,2,4,5,6,8 right}backslash left{ a,b right}

Suy ra trong trường hợp này có 1.6.5.4=120 số.

TH 2:
dne 0Rightarrow din left{ 2,4,6,8 right}Rightarrow  có 4 cách chọn d

Với mỗi cách chọn d, do ane 0 nên ta có 5 cách chọn

ain left{ 1,2,4,5,6,8 right}backslash left{ d right}.

Với mỗi cách chọn a,d ta có 5 cách chọn bin left{ 1,2,4,5,6,8 right}backslash left{ a right}

Với mỗi cách chọn a,b,d ta có 4 cách chọn cin left{ 1,2,4,5,6,8 right}backslash left{ a,b right}

Suy ra trong trường hợp này có displaystyle 4.5.5.4=400 số.

Vậy có tất cả 120+400=520 số cần lập.

Cách 2: Tính gián tiếp ( đếm phần bù)

Gọi A={ số các số tự nhiên có bốn chữ số đôi một khác nhau được lập từ các số displaystyle 0,1,2,4,5,6,8}

B={ số các số tự nhiên lẻ có bốn chữ số đôi một khác nhau được lập từ các số displaystyle 0,1,2,4,5,6,8}

C={ số các số tự nhiên chẵn có bốn chữ số đôi một khác nhau được lập từ các số displaystyle 0,1,2,4,5,6,8}

Ta có: left| C right|=left| A right|-left| B right|.

Dễ dàng tính được: left| A right|=6.6.5.4=720.

Ta đi tính left| B right|?
x=overline{abcd} là số lẻ Rightarrow din left{ 1,5 right}Rightarrow d có 2 cách chọn.

Với mỗi cách chọn d ta có 5 cách chọn a(vì ane 0,ane d)
Với mỗi cách chọn a,d ta có 5 cách chọn b

Với mỗi cách chọn a,b,d ta có 4 cách chọn c

Suy ra left| B right|=2.5.5.4=200

Vậy left| C right|=520.

Ví dụ 2: Cho tập A=left{ 0,1,2,3,4,5,6 right}

a) Từ tập A ta có thể lập được bao nhiêu số tự nhiên gồm 4 chữ số đôi một khác nhau

    A.720                     B.261                      C.235                      D.679

b) Từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số và chia hết cho 5.

    A.660                     B.432                      C.679                      D.523

Lời giải:

1. Gọi số cần lập x=overline{abcd}, a,b,c,din left{ 0,1,2,3,4,5,6 right};ane 0

Chọn a: có 6 cách; chọn b,c,d có 6.5.4

Vậy có 720 số.

2. Gọi x=overline{abcde} là số cần lập, ein left{ 0,5 right},ane 0

bullet e=0Rightarrow e có 1 cách chọn, cách chọn a,b,c,d:6.5.4.3

Trường hợp này có 360 số

e=5Rightarrow e có một cách chọn, số cách chọn a,b,c,d:5.5.4.3=300

Trường hợp này có 300 số

Vậy có 660 số thỏa yêu cầu bài toán.

Ví dụ 3: Tính tổng các chữ số gồm 5 chữ số khác nhau được lập từ các số 1, 2, 3, 4, 5?

    A. 3999960             B. 33778933             C. 4859473             D. 3847294

Lời giải:

Chọn A. 

Có 120 số có 5 chữ số được lập từ 5 chữ số đã cho.

Bây giờ ta xét vị trí của một chữ số trong 5 số 1, 2, 3, 4, 5 chẳng hạn ta xét số 1. Số 1 có thể xếp ở 5 vị trí khác nhau, mỗi vị trí có 4!=24 số nên khi ta nhóm các các vị trí này lại có tổng là : displaystyle 24left( {{10}^{4}}+{{10}^{3}}+{{10}^{2}}+10+1 right)=24.11111
Vậy tổng các số có 5 chữ số là : displaystyle 24.11111left( 1+2+3+4+5 right)=3999960.

Leave a Comment